UNIJUÍ – UNIVERSIDADE REGIONAL DO
NOROESTE DO ESTADO DO RIO GRANDE DO SUL
CURSO DE CAPACITAÇÃO DE PROFESSORES DA
ÁREA DE CIÊNCIAS DA NATUREZA MATEMÁTICA E SUAS TECNOLOGIAS
DISCIPLINA: Modelagem Matemática
PROFESSORA: Denise Knorst da Silva
MODELANDO COM A MATEMÁTICA

ALUNA Luciane Maria Santos da
Silva
Cachoeira do Sul, abril de 2006
MODELANDO COM
A MATEMÁTICA
OBJETIVOS
- Interagir com o coletivo escolar;
- Reelaborar concepções acerca do processo ensino aprendizagem de matemática;
- Apresentar uma alternativa para interagir com as disciplinas de Física, Biologia e Química;
- Aprofundar conhecimentos sobre Modelagem Matemática;
- Apresentar formas de implementação da modelagem;
- Reconhecer a viabilidade da modelagem para a Educação Básica;
INTRODUÇÃO
Neste trabalho apresento um estudo referente ao processo de cálculo da necessidade diária de calorias (cal) de cada aluno, bem como, o gasto de calorias na realização de algumas atividades físicas, como objeto de estudo para a aplicação da Modelagem Matemática. Este tema foi escolhido com o intuito de aproximar o ensino da Matemática ao cotidiano dos alunos do segundo ano do Ensino Médio como uma proposta de ensino integrado como as disciplinas de Física, Química e Biologia.
Pretendo dessa forma, motivar o aluno para que perceba a Matemática como um instrumento útil na resolução de muitos problemas práticos. Além disso, busquei informações referentes à quantidade de calorias necessárias e a relação com o gasto de energia em algumas atividades físicas visando despertar no aluno a necessidade de uma alimentação adequada e balanceada, bem como a prática de exercícios para manter uma vida saudável.
1. JUSTIFICATIVA
Sabendo-se da importância da escola em observar a realidade cultural dos alunos e formar pessoas criativas e com habilidade em associar o cotidiano com conteúdos matemáticos para tornar o processo ensino aprendizagem mais fácil propus-me a fazer este trabalho desenvolvendo este tema.
O corpo humano necessita da energia (calorias) fornecida pelos alimentos para o desempenho de funções como metabolismo do descanso, atividades físicas, entre outros. E a relação deste consumo com o gasto de calorias é que nos fará emagrecer ou engordar.
Mais do que uma questão de estética e saúde, a boa forma pode ajudar a garantir um bom emprego, um bom desempenho nas atividades físicas, uma ótima auto-estima. É inegável que num primeiro momento a aparência física é que chama a atenção, o que desfavorece quem está acima do peso. Como se isto não bastasse, a baixa auto-estima gera um conflito interno atrapalhando a realização de vários objetivos de vida (emprego novo, uma nova turma de amigos, um baile tão sonhado ou talvez aquele vestido lindíssimo da vitrine).
Contar o valor
calórico que consome parece ser uma ótima alternativa de manter o peso,
controlar o seu cardápio e buscar alternativa quando extrapolou o limite.
Tentando fazer uma reeducação alimentar, pois não há restrições na ingestão de
alimentos.
2. PESQUISA DE CAMPO
2.1. Método
Para a realização deste trabalho utilizamo-nos dos métodos quantitativo e qualitativo, por apresentarmos um problema com seus dados a serem analisados e resolvidos pelos alunos, onde os dados serão demonstrados estatisticamente.
Para a realização deste trabalho, primeiramente, foi aplicado um questionário com os alunos da turma 202 da escola (Apêndice A).
O questionário, segundo Kude (2001), é um instrumento através do qual o pesquisador pode utilizar-se para sua coleta de dados e permite refletir os interesses do pesquisador, ou seja, procura reconhecer e levar em conta seus próprios vieses para melhor lidar com os mesmos.
2.2. Participantes
A pesquisa foi realizada em uma escola pública localizada na periferia de uma cidade do interior do Rio Grande do Sul.
Realizou-se em uma turma do Ensino Médio (2ª série), constituída por nove alunos, com faixa etária entre 15 a 24 anos.
2.3. Procedimentos para coleta de dados
O procedimento de coleta de dados envolveu:
a) Questionário com os alunos: foi aplicado um questionário na turma pesquisada que continha quatorze questões objetivas. (Apêndice A).
2.4. Procedimento para análise de dados
Após a aplicação do questionário, foi realizada a análise quantitativa das respostas fornecidas pelos participantes da pesquisa. Os dados foram codificados e apresentados em tabelas (Apêndice B) e gráficos (Apêndice C). Utilizando-se como uma das medidas quantitativas da pesquisa as medidas de tendência central e de dispersão.
Os achados estão descritos na discussão da investigação.
3. INVESTIGAÇÃO
A idéia de analisar este problema surgiu na observação dos alunos no período do recreio, onde os mesmos não optavam por lanches saudáveis ou até mesmo não ingeriam nenhum tipo de alimento e na constatação de que a maioria dos alunos do ensino médio não gosta de praticar Educação Física.
O início do trabalho deu-se com a observação dos alunos durante o intervalo das aulas, aplicação de um questionário (Apêndice A).
Após a coleta de dados junto aos alunos, os mesmos foram analisados e apresentados aos alunos (Tabela 1), o resultado está descrito abaixo. Os alunos optaram por dar ênfase no que diz respeito às respostas marcadas e de relevância para o propósito a que se destina este trabalho, ou seja, levantar dados onde se possibilite o cálculo das calorias necessárias a cada um, bem como, levantamento de alternativas para controle de suas calorias para que viva melhor e com mais disposição.
Questionário aplicado com os alunos do 2ª série do Ensino Médio
|
Tabela 1:
Pesquisa de dados Turma 202, maio/2006, Cachoeira do Sul |
|
|
|
|
|
|
|
|
||||||
|
Entrev. |
Idade |
Sexo |
Peso |
Altura |
Freq. At. Fis |
Tipo At. Fis |
Fez Reg. |
Qual |
IMC |
Alim Bal. |
Peso cor. |
TMB |
Cal nec. |
Cál. Cal. |
|
1 |
17 |
1 |
55 |
160 |
2 |
4 |
2 |
0 |
2 |
2 |
3 |
2 |
2 |
2 |
|
2 |
24 |
1 |
59 |
152 |
1 |
1 |
1 |
4 |
2 |
1 |
2 |
2 |
2 |
2 |
|
3 |
16 |
2 |
0 |
0 |
2 |
5 |
1 |
4 |
2 |
3 |
3 |
2 |
2 |
2 |
|
4 |
16 |
1 |
50 |
160 |
2 |
4 |
2 |
0 |
2 |
1 |
3 |
2 |
2 |
2 |
|
5 |
16 |
2 |
70 |
185 |
2 |
4 |
2 |
0 |
2 |
1 |
2 |
2 |
2 |
2 |
|
6 |
16 |
2 |
62 |
178 |
3 |
5 |
2 |
0 |
2 |
1 |
2 |
2 |
2 |
2 |
|
7 |
15 |
1 |
49 |
160 |
2 |
2 |
2 |
0 |
2 |
1 |
3 |
2 |
2 |
2 |
|
8 |
16 |
1 |
44 |
151 |
3 |
2 |
2 |
0 |
1 |
1 |
2 |
2 |
1 |
1 |
|
9 |
17 |
1 |
73 |
155 |
2 |
5 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1) Idade dos alunos:
Xi = 17-24-16-16-16-16-15-16-17
rol = 15-16-16-16-16-16-17-17-24
X = ∑ = rol = 153
= 17
n
9 9
Em média a idade dos nove alunos da turma é 17 anos.
Na análise a moda é 16 anos.
2) Sexo dos alunos:
66,7 % dos alunos são do sexo feminino e 33,3 % são do sexo masculino.
3)Peso dos alunos:
Xi = 55-59-00-50-70-62-49-44-73
rol = 00-44-49-50-55-59-62-70-73
X = ∑ = rol = 462 =
57,75
n 8 8
Em média o peso dos alunos é 57,75 quilogramas.
4) Altura dos alunos em centímetros:
Xi= 160-152-00-160-185-178-160-151-155
rol = 00-151-152-155-160-160-160-178-185
X = ∑ = rol = 1301
= 163
n 8 8
Em média a altura dos alunos é 163 centímetros.
5) Freqüência de prática de atividade física
|
Tabela 1: Distribuição do sexo de acordo com pratica de
atividade física da Turma 202
maio/2006 |
|||||||
|
|
|
|
Sexo |
|
|
|
|
|
|
Dados |
Freq. At.
Fis |
Feminino |
Masculino
|
Total
geral |
|
|
|
|
nº.
alunos |
não
pratica |
1 |
|
1 |
|
|
|
|
|
até 4 h/
semana |
4 |
2 |
6 |
|
|
|
|
|
de 4 a 10
h/ semana |
1 |
1 |
2 |
|
|
|
|
% de
alunos |
não
pratica |
16,67% |
0,00% |
11,11% |
|
|
|
|
|
até 4 h/
semana |
66,67% |
66,67% |
66,67% |
|
|
|
|
|
de 4 a 10
h/ semana |
16,67% |
33,33% |
22,22% |
|
|
|
|
Total nº.
alunos |
|
6 |
3 |
9 |
|
|
|
|
Total %
de alunos |
100,00% |
100,00% |
100,00% |
|
|
|
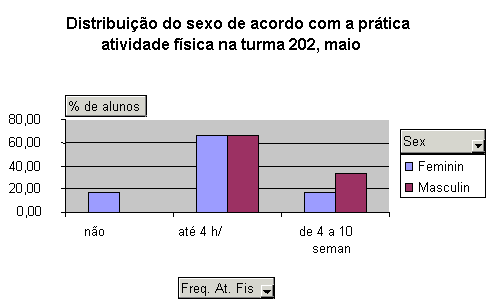
Analisando a tabela e o gráfico verificamos que na turma:
- 16,67 % (uma aluna) do sexo feminino não praticam atividade física e que todos os meninos praticam atividade física;
- 66,67% (quatro alunas) do sexo feminino e 66,67 (dois alunos) do sexo masculino praticam atividade até 4 horas por semana;
- 16,67% (uma aluna) do sexo feminino e 33,33 (um aluno) do sexo masculino praticam atividade de 4 a 10 horas por semana.
6) Tipo de atividade física:
De acordo com a análise da tabela:
- 11,11 % dos alunos não fazem nenhuma atividade física;
- 22,23 % dos alunos fazem caminhada;
- Nenhum aluno pratica corrida;
- 33,33 % dos alunos praticam jogos;
- 33,33 % dos alunos praticam Educação Física.
7)Regime alimentar e 8) Tipo de regime:
Observando a tabela verificamos que:
- 66,67 % dos alunos nunca fizeram regime alimentar;
- 33,33% dos alunos fizeram regime alimentar, sendo que destes 66,67 % fez regime sem orientação e 33,33 % copiou o regime de revistas ou livros.
9) Cálculo do IMC (Índice de Massa Corporal):
De acordo com os resultados demonstrados na tabela:
- 88,89 % dos alunos não sabem calcular seu Índice de Massa Corporal;
- 11,11 % dos alunos sabem calcular seu Índice de Massa Corporal.
10) Alimentação Balanceada
Pela análise dos resultados observamos que:
- 66,67 % dos alunos sabem o que é uma alimentação balanceada;
- 22,22 % dos alunos não sabem o que é alimentação balanceada;
-11,11 % nunca se preocuparam em saber como é uma alimentação balanceada.
11) Peso correto:
- 55,56 % dos alunos não sabem se possuem peso correto;
- 44,44 % dos alunos nunca se preocuparam em saber se possuem peso correto.
12) Taxa de Metabolismo Basal (TMB):
- 100 % dos alunos não sabem o que é Taxa de Metabolismo Basal.
13) Quantidade e 14) Cálculo de calorias necessárias:
- 88,89 % dos alunos não sabem que quantidade de calorias deve ingerir nem como calcular para manter seu peso;
- 11,11% dos alunos sabem que quantidade de calorias deve ingerir nem como calcular para manter seu peso.
4. PROBLEMATIZAÇÃO
Problema 1
4.1. Como se calcula o valor energético total (VET)?
O valor energético total é a quantidade de energia, de origem alimentar, necessária para cobrir as perdas do organismo vivo nas 24 horas do dia.
Compreende os requerimentos energéticos do organismo que provém da soma de três fatores:
>> metabolismo basal: quota energética constante ou básica; quantidade mínima necessária para se manter vivo.
>> metabolismo do trabalho: (ou de atividade): quantidade de calorias exigidas pelo trabalho físico e que deve ser acrescido ao metabolismo basal.
>> ação dinâmico-específica: aumento da produção de calor motivada pela ingestão de alimentos, pelo processo digestivo e transformações que os nutrientes sofrem durante o metabolismo.
Para sabermos quantas calorias podemos comer no dia, é preciso fazer algumas contas. Aliás, o ideal é que se confira o resultado, repetindo a operação por segurança. A seguir explicação de etapa por etapa do cálculo.
4.1.1. Qual é a sua taxa de
metabolismo basal (TMB)?
Metabolismo é a soma de processos físicos e químicos que se desenvolvem no organismo vivo, pelo qual as células convertem as substâncias nutritivas em energia útil, calor e trabalho à síntese de novos compostos vitais para estruturação e funções celulares.
Constitui assim, um complexo total, contínuo, de trocas químicas, que determinam a utilização final dos nutrientes individualmente, pois todas as células requerem permanente fornecimento de nutrientes. Possui duas fases:
Ø Anabolismo – diz respeito à síntese de novos compostos, para o crescimento, manutenção e reparo dos tecidos; é um processo CONSTRUTIVO.
Ø Catabolismo - é o processo pelo quais as moléculas dos nutrientes são degradadas, liberando energia, seguido de subseqüente eliminação do produto de degradação. É um processo DESTRUTIVO.
Esses processos acontecem simultaneamente no organismo. Quando o anabolismo excede o catabolismo ocorre crescimento. Quando é o contrário, o processo de desnutrição é mais rápido que o de construção, levando á perda de substâncias e peso.
O balanço entre as reações catabólicas e anabólicas nos tecidos orgânicos encontra-se sob controle de enzimas celulares, suas coenzimas, outros fatores e hormônios.
A taxa de metabolismo basal é definida como quota energética básica; é a energia necessária para a vida vegetativa, para mater a temperatura corpórea, dar suporte para o trabalho muscular do coração e músculos respiratórios e finalmente, suprir as necessidades mínimas dos tecidos em repouso.
Revela o quanto seu organismo gasta quando está em repouso. Você gasta energia até mesmo quando tem um pensamento.
Os fatores que alteram a taxa de metabolismo basal são: idade, massa magra corpórea, temperatura, hormônios, drogas (anestésicos, cafeína), estado emocional e estresse.
Existem algumas equações para estimar a TMB de um indivíduo. Optei pela equação proposta pela Organização mundial da Saúde.
Para mulheres
|
10 a 18 anos |
12,2 x peso (kg) + 746 |
|
18 a 30 anos |
14,7 x peso (kg) + 496 |
|
30 a 60 anos |
8,7 x peso (kg) + 829 |
|
Acima de 60 anos |
10,5 x peso (kg) + 596 |
Para homens
|
10 a 18 anos |
17,5 x peso (kg) + 651 |
|
18 a 30 anos |
15,3 x peso (kg) + 679 |
|
30 a 60 anos |
8,7 x peso (kg) + 879 |
|
Acima de 60 anos |
13,5 x peso (kg) + 487 |
Cada aluno fez o cálculo da sua TMB , vamos acompanhar os modelos matemáticos utilizando os dados do entrevistado 1:
-Uma mulher de 17 anos, com 1,60 metros de altura e 55 kg, que estuda e pratica atividade física no período de até 4 horas por semana.
TMB = 12,2 x peso (kg) + 746 = 12,2 x 55 + 746 = 671 + 746 = 1417
TMB = 1417
4.1.2. Qual é a sua necessidade
diária de energia?
Energia é definida como capacidade de executar trabalho ou produzir mudanças na matéria. A energia química obtida dos alimentos é usada para o trabalho muscular, para a atividade cerebral e nervosa e para a síntese de tecidos corpóreos.
Caloria é a unidade de energia usada em nutrição que expressa a energia fornecida pelos nutrientes ao serem metabolizados.
Nessa fase do cálculo, o aluno descobrirá quanto seu organismo gasta para ficar com o peso que está – portanto, ainda não será o valor de que você precisa para emagrecer.
Consultando a tabela abaixo e encontrando o perfil, de acordo com a Organização Mundial de Saúde, o número correspondente será o fator de atividade (FA):
|
mulher |
homem |
|
|
1,2 |
1,2 |
*
dia-a-dia muito sedentário sem atividade física |
|
1,3 |
1,3 |
*
dia-a-dia movimentado sem atividade física programada ou *
dia-a-dia parado atividade física programada 3x por
semana, 30 min por dia |
|
1,35 |
1,4 |
*
dia-a-dia movimentado atividade física programada 3x por semana,
30 min por dia |
|
1,45 |
1,5 |
*
dia-a-dia movimentado atividade física programada 3x por semana,
mais de 1 hora. ou *
atividade física programada diária, por mais de 30 minutos |
|
1,5 |
1,6 |
*
dia-a-dia movimentado atividade física programada diária, por 1
hora a 2 horas e meia |
|
1,7 |
1,8 |
*
dia-a-dia movimentado atividade física programada diária, por
mais de 3 horas |
A sua necessidade diária de energia será:
Taxa de metabolismo basal multiplicado pelo seu fator de atividade, ou seja:
TMB X FA
Exemplo do entrevistado 1:
TMB= 1417 e FA= 1,3
TMB X FA = 1842,1
4.1.3.Qual o seu índice de massa corporal
(IMC)?
A OMS (Organização Mundial de Saúde) passou a recomendar na avaliação do estado nutricional o IMC – Índice de Massa Corpórea, obtido pela fórmula:
IMC= peso em quilo dividido por sua altura ao quadrado
IMC= peso (kg)
altura (m) x altura (m)
De acordo com os dados do nosso entrevistado:
IMC=
55
1,60m x 1,60m
IMC= 55
2,56 m
IMC = 21,5
- IMC adequado conforme idade:
|
Grupo etário/ anos |
IMC em kg/m² |
|
19 – 24 |
19 – 24 |
|
25 – 34 |
20 – 25 |
|
35 – 44 |
21 – 26 |
|
45 – 54 |
22 – 27 |
|
55 – 64 |
23 – 28 |
|
65 ou
mais |
24 – 29 |
- Valores do IMC elevado para o adulto
|
Índice >
25 |
Indica
sobrepeso |
|
Índice >
30 |
Indica
obesidade |
|
Índice >
40 |
Indica
obesidade mórbida |
4.1.4. Qual o seu limite de
calorias para manter-se no peso?
Consultando a tabela abaixo e subtraindo o valor correspondente o aluno encontrará afinal o correspondente ao seu valor energético total.
Ou seja, o valor de calorias que deve comer, no máximo, para manter-se no peso.
|
IMC |
mulher (cal) |
homem (cal) |
|
Entre 15 e 19,9 |
450 |
540 |
|
Entre 20 e 24,9 |
540 |
630 |
|
Entre 25 e 29,9 |
630 |
720 |
|
Entre 30 e 34,9 |
720 |
810 |
|
Entre 35 e 39,9 |
900 |
990 |
|
Maior que 40 |
1080 |
1170 |
Limite de calorias = (TMB x FA) – cal da tabela de acordo com o IMC
O limite de calorias da entrevistada um, de acordo com os dados é;
(TMB x FA) – 540 =
1842,1 – 540 = 1302,1 kcal
O valor energético total do entrevistado, ou seja para manter o peso preservando o mesmo fator de atividade; é 1302,1 kcal por dia.
Problema 2
4.2. Quantas calorias você
consumiu no lanche da tarde?

Na sala de aula foi montada uma mesa para o lanche da tarde dos alunos. Cada aluno organizou seu lanche conforme o gosto. Posteriormente a professora perguntou quem saberia quantas calorias foi consumida e como encontrar este valor.
A partir destas informações desencadeou-se o processo de investigação do problema pelos alunos. Ao professor coube orientar o processo disponibilizando material para pesquisa.
Quadro 1 – Valor calórico de alguns alimentos
|
NOME |
PORÇÃO |
CALORIAS |
|
|
|
|
|
LEITE E DERIVADOS |
|
|
|
Leite integral |
1 copo 200 ml |
126 kcal |
|
Queijo mussarela |
1 fatia |
72 kcal |
|
Requeijão tradicional |
1 colher sopa |
216 kcal |
|
Iogurte natural |
1/2 copo |
216 kcal |
|
Creme de leite |
1 colheres sopa |
108 kcal |
|
Maionese |
1 colher sopa |
126 kcal |
|
|
|
|
|
PÃES E BOLACHAS |
|
|
|
Pão de forma |
1 fatia |
108 kcal |
|
Pão italiano |
1 fatia |
108 kcal |
|
Pão francês com miolo |
1 unidade |
144 kcal |
|
Pão francês sem miolo |
1 unidade |
108 kcal |
|
Pão de centeio |
1 fatia |
72 kcal |
|
Bolacha água e sal |
1 unidade |
36 kcal |
|
Bolacha recheada |
1 unidade |
54 kcal |
|
Torrada |
2 unidades |
108 kcal |
|
|
|
|
|
BEBIDAS |
|
|
|
Café preto |
à vontade |
0 kcal |
|
Refrigerante |
1 copo 200 ml |
83 kcal |
|
Suco de laranja |
1 copo 200 ml |
108 kcal |
|
Bebida energética |
1 lata média |
122 kcal |
|
|
|
|
|
FRIOS |
|
|
|
Mortadela de frango |
1 fatia |
18 kcal |
|
Mortadela suina |
1 fatia |
54 kcal |
|
Presunto magro |
1 fatia |
18 kcal |
|
|
|
|
|
DOCES |
|
|
|
Bolo de laranja |
1 fatia fina |
216 kcal |
|
Doce de goiaba |
1 colher sopa |
72 kcal |
|
Doce de leite |
1 colher sopa |
100 kcal |
|
Leite condensado |
1 colher sopa |
65 kcal |
|
|
|
|
|
VERDURAS |
|
|
|
Alface, espinafre, couve, mostarda, tomate |
à vontade |
0 kcal |
|
Abobora, brócolis, cenoura, chuchu. Vagem |
2 colheres sopa |
36 kcal |
|
Fonte: A
Dieta dos Pontos - Alfredo Halpern |
|
|
Quadro 2 – Exemplo do entrevistado 1 – Lanche da tarde:
|
NOME |
PORÇÃO |
CALORIAS |
|
Refrigerante |
1 copo 300 ml |
124 ,5 kcal |
|
Pão de forma |
3 fatias |
324 kcal |
|
Mortadela |
1 fatia |
18 kcal |
|
Queijo mussarela |
1 fatia |
72 kcal |
|
Creme de leite |
2 colheres sopa |
216 kcal |
|
Tomate |
3 rodelas |
0 kcal |
|
Alface |
2 folhas |
0 kcal |
|
Bolo de laranja |
1 fatia |
216 kcal |
|
TOTAL |
|
970,50 kcal |
Após esta atividade os alunos deverão anotar os valores correspondentes ao total de calorias consumidas no dia da atividade:
Exemplo da aluna já citada:
CM: calorias do café da manhã = 287 kcal
LM: calorias do lanche da manhã = 54 kcal
A: calorias do almoço = 892,8 kcal
L: calorias do lanche da tarde = 970, 50 kcal
J: calorias do jantar ( repetiu o café da manhã e mais tarde bebeu um copo de leite com Nescau = 458 kcal
TOTAL DE CALORIAS DIARIA: CM + LM + A + L + J
TCD = 2262,3 kcal
Diferencial =2662,3 kcal – 1302,1 kcal = 1360,2 kcal
A aluna do exemplo estudado consumiu excesso de calorias no valor de 1360,20 kcal.
4.3.Calorias a queimar – correr
ou caminhar?
Quadro 3 – Quantidade de calorias queimadas enquanto correndo e caminhando
|
|
Calorias totais / km |
Calorias líquidas/ km |
|
Corrida |
1,0 x peso (em kg) |
0,86 x peso (em kg) |
|
Caminhada |
0,72 x peso (em kg) |
0,41 x peso (em kg) |
|
Fonte: Revista Runner’s World Dez 2004 |
|
|
Usando as fórmulas acima é possível determinar a quantidade de calorias queimadas enquanto correndo e caminhando. Calorias líquidas significam o total de calorias queimadas menos o metabolismo basal. Os cientistas consideram esta a melhor maneira de avaliar a queima de calorias em qualquer exercício.
Se você pensa que correr e caminhar queima a mesma quantidade de calorias por km, é melhor deixar de lado aquela bolachinha recheada.
1- Demonstrar o gasto de calorias líquidas da turma comparando as duas opções correr ou caminhar
|
Tabela
2 Gasto de calorias líquidas da Turma
202, maio de 2006 |
|||
|
Peso |
Caminhada |
Corrida |
|
|
|
0,41 x peso |
0,86 x peso |
|
|
0 |
0 cal/ km |
0 cal/ km |
|
|
44 |
18,04 cal/km |
37,84 cal/km |
|
|
49 |
20,09 cal/km |
42,14 cal/km |
|
|
50 |
20,50 cal/km |
43,00 cal/km |
|
|
55 |
22,55 cal/km |
47,30 cal/km |
|
|
59 |
24,19 cal/km |
50,74 cal/km |
|
|
62 |
25,42 cal/km |
53,32 cal/km |
|
|
70 |
28,70 cal/km |
60,20 cal/km |
|
|
73 |
29,93 cal/km |
62,78 cal/km |
|
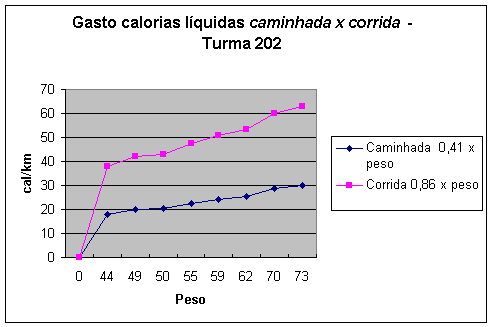
A interpretação dos dados por meio da análise do gráfico permite concluir que a queima líquida de calorias correndo (6 min/km) é duas vezes maior do que caminhando (12 min/km). Considerando-se que, num determinado tempo, você percorre, correndo, o dobro da distância que percorreria caminhando, podemos dizer que correr queima quatro vezes mais calorias por hora do que caminhar.
Uma verdade amplamente divulgada, repetida e aceita pela maioria dos corredores é que caminhar e correr queima o mesmo número de calorias por km, pois ambas as atividade requerem mover o mesmo peso pela mesma distância, realizando o mesmo trabalho ( conforme disse Isaac Newton).
Os corredores sempre ouviram dizer que correr queima cerca de 100 calorias por milha, ou, mais precisamente, 1 caloria por kg de peso por km percorrido (caminhando ou correndo).
Uma pesquisa recente contraria essa verdade. Conforme artigo publicado em dezembro de 2004 no “Medicine & Science in Sports & Exercise”, jornal oficial do “American College of Sports Medice”, um grupo de pesquisadores da Universidade de Siracusa mediu a quantidade real de calorias queimadas por homens e mulheres ao correr e caminhar 1600 metros.
Resultado: Os homens queimaram uma média de 124 calorias correndo e apenas 88 caminhando, as mulheres queimaram 105 e 74. Os homens queimaram mais que as mulheres por pesarem mais.
Este resultado indica que 40 % a mais de calorias são queimadas correndo do que caminhando a mesma distância.
Uma possível explicação de porque os resultados diferem da interpretação simplista da lei de Movimento de Newton é que caminhar e correr não são atividades tão compatíveis quanto se imagina. Correr envolve saltar continuamente de um pé para outro, elevando e abaixando o centro de gravidade do corpo em cada passada, o que requer grande quantidade de força newtoniana para vencer a força da gravidade.
Os números acima se referem á “Queima Total de Calorias” durante o exercício. Muito mais relevante é a “Queima Líquida de Calorias”, obtida subtraindo-se da Queima Total as calorias referentes ao metabolismo basal, isto é, aquelas calorias que seu corpo teria queimado durante o mesmo tempo se você estivesse permanecido em repouso num sofá.
Assim, é possível concluir, mediante a utilização do modelo, que correr queima mais calorias do que caminhar. A pesquisa não significa que caminhar queima agora menos calorias do que antes. Significa apenas que os caminhantes precisam caminhar um pouco mais ou comer um pouco menos para atingirem seus objetivos.
Segundo Nick Feranson, experiente maratonista – “Para quem não é aficionado em corridas, caminhar é um excelente exercício. Acho que mesmo os corredores poderiam, para variar, correr de vez em quando – uma vez por ano”.
5. DISCUSSÃO DOS RESULTADOS
Quando escolhemos o tema “MODELANDO COM A MATEMÁTICA”, tínhamos como objetivo investigar como é calculada a quantidade de calorias necessárias para uma pessoa se manter no peso e, se fora do peso, buscar alternativas para se “modelar”. A finalidade desta investigação não era apenas realizar a modelagem matemática, mas também realizar um trabalho de conscientização com relação ao tratamento da obesidade, que hoje é um problema mundial, inclusive na infância, e também estimular a prática de atividades físicas para uma melhor qualidade de vida.
Nas primeiras investigações que fizemos pudemos verificar que a turma, a pesar de saber o que é uma alimentação balanceada, não utiliza este conhecimento no seu cotidiano, pois na hora da atividade da construção do seu lanche da tarde não levaram isto em conta. Através de conversas informais chegamos à conclusão de que a realização de uma atividade física ocorre só na escola e somente por ela ser obrigatória.
Mesmo a turma estar em média com um peso adequado os alunos não sabiam como calcular o valor energético total ou seja quantas calorias deveriam ingerir para manterem-se no peso. Nem sabiam optar por uma atividade extra, além da Educação Física, para o gasto das energias.
Através do modelo matemático utilizando a coleta de dados e a aplicação de fórmulas próprias que evolveram as operações matemáticas básicas , encontramos a solução do nosso primeiro problema. O segundo problema que se refere ao consumo e gasto de calorias foram resolvidos através de modelos matemáticos que envolveram coleta de dados, média, razão, regra de três, análise de tabelas e gráficos.
A modelagem matemática é uma metodologia alternativa que possibilita modificar a prática na sala de aula, onde a matemática trabalhada com os alunos parte das situações vivenciadas no dia-a-dia, permitindo também trabalhar a transversalidade e a interdisciplinaridade, acontecendo o ensino-aprendisagem como um todo.
Percebemos que trabalhar o tema “MODELANDO COM A MATEMÁTICA” com alunos do ensino médio desenvolvendo a arte de modelagem matemática seria um trabalho muito significativo. Conteúdos como funções, plano cartesiano, análise e construção de tabelas e gráficas, volume de figuras espaciais, estatística, análise combinatória poderiam ser trabalhados a partir deste estudo, no qual conteúdos do ensino fundamental como regras de três, sistema de medidas e razão estariam sendo revisados de uma forma intrigante. Além de ser um trabalho interdisciplinar juntamente com a Física, Química e Biologia. Ainda, estaríamos desenvolvendo um trabalho riquíssimo de conscientização em relação ao problema de obesidade. Problema tão sério este que o número de cirurgias bariáticas aumenta a cada dia.
Cabe ainda destacar que o tema que escolhemos é rico em informações matemáticas podendo ser desenvolvidas muito outras problematizações e modelagens matemáticas.
6. BIBLIOGRAFIA
- CASPANI, Denise Carvalho, Nutrição e Ditética , Cachoeira do Sul, EEPS (Escola de Educação Profissional em Saúde), 2004
- BURFOOT, Amby, Quantas calorias está queimando? , Runner’s World, 2005
- HALPERN, Alfred, BEYRUTI, Mônica & MONEGAGLIA, Ana Paula, Dieta dos Pontos, São Paulo, Abril, 2005
- Sites: www.cyberdiet.com.br
- ____: www.drashirleydecampos.com.br