UNIJUÍ– UNIVERSIDADE REGIONAL DO NOROESTE DO ESTADO DO RIO GRANDE DO SUL 

DeFEM– Departamento De Física, Estatística E Matemática

Licenciatura em Matemática – Disc. Modelagem Matemática I  Prof. Pedro Augusto Pereira Borges
  

Adriana Inês Mossmann, Janice Maria Maldaner, Sidmara Blaszak

1 - INTRODUÇÃO 

            O presente trabalho é resultado de uma pesquisa de campo e bibliográfica, sendo o mesmo importante para se trabalhar a interdisciplinaridade, bem como para se ter uma alternativa no ensino de matemática, que busque novos caminhos e desperte o interesse, o gosto e a aprendizagem dos alunos. Consta no presente trabalho, o tema, “cubagem de madeira”, realizada através de uma pesquisa de campo, envolvendo medições e cálculos de volume por métodos populares e científicos, bem como demonstração de fórmulas. O trabalho aborda tópicos de matemática vistos nas séries do ensino fundamental, de forma prática. Aborda-se desde os conceitos mais simples das quatro operações fundamentais usados nos cálculos de volumes, até as demonstrações de fórmulas através da álgebra , geometria e relações com funções visualizadas através de gráficos. 

2 – DESCRIÇÃO DA MODELAGEM MATEMÁTICA

COMO MEDIR OS DIÂMETROS DE UM TRONCO DE ÁRVORE? 

            Usando trena, escada, e esquadros, efetuou-se a medição de uma árvore de pinheiro escolhido para facilitar a análise dos volumes, por ter um tronco praticamente cilíndrico. 
Iniciou-se o trabalho medindo a árvore (sem ser derrubada) até a altura que permitia a escada colocada, ou seja 3 m. A seguir, medindo a circunferência da mesma, na base,a 1,5 m e na altura de 3 m e o diâmetro, usando duas estacas, segurando-as paralelamente efetuando a medição, verificou-se que havia significativa margem de erro, pois ao fazer a divisão da circunferência pelo valor do diâmetro obtido não verificou-se um valor muito próximo ao número π . 

            Com isso, constatou-se que este método para medir o diâmetro não é nada preciso, pois dificilmente as estacas serão colocadas paralelamente. 
Então, seguindo a sugestão do professor, realizou-se nova medição, com o uso de 2 esquadros, confeccionados usando ripas de madeira, um maior e outro menor. Segurando o esquadro maior de forma que o tronco da árvore fique encaixado no ângulo e deslizando o outro paralelamente ao primeiro até encostar ao tronco, pudemos efetuar a medição obtendo valores mais exatos, o que se pode verificar no quadro abaixo. 

CIRCUNFERÊNCIA MAIOR = 1,76 m
CIRCUNFERÊNCIA MÉDIA = 1,60 m
CIRCUNFERÊNCIA MENOR = 1,50 m 
Quadro comparativo entre valores de diâmetros obtidos através de medições e pela relação matemática C / D = π. 

DIÂMETRO DO ESQUADRO	C / π = D
0,56 m	0,56 m
0,51 m	0,50 m
0,48 m	0,47 m

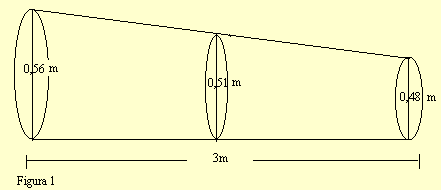
            Usando as medidas obtidas , conforme mostra a figura 1, e efetuando o cálculo da cubagem da madeira de diferentes formas pesquisadas através de entrevistas e estudos bibliográficos encontram-se resolvidos os seguintes problemas:

PROBLEMA 1:  COMO CALCULAR O VOLUME DE UM TRONCO DE ÁRVORE? 

1º) MODELO DO MADEIREIRO 

Este senhor entrevistado, é dono de uma serraria e marcenaria. Nessas atividades, efetua a compra das toras, serra-as vendendo a madeira para construções e /ou para a industrialização na fabricação de aberturas.   Contribuiu para este trabalho, explicando como faz a cubagem da madeira que compra para comercialização. Seu, método, consiste em transformar a tora em um paralelepípedo. Para tal, considera as perdas num total de 25% o qual é descontado do valor do diâmetro médio da tora que passa a ser largura e altura do paralelepípedo.

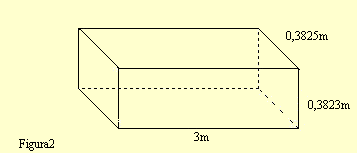
Diâmetro médio 0,51 m – 25% de 0,51m = 0,3825m 
V = [0,51m x (100/100-25/100)]2 x 3m = 0,43892 m³ 
Logo, o modelo matemático 1 será: 
V = (D x 0,75)² x L , onde V é volume da tora , D a medida do diâmetro médio menos 25% de desta medida e L a medida do comprimento da tora. 

2º) MODELO DO ENGENHEIRO FLORESTAL 

O engenheiro florestal entrevistado, é dono de uma madeireira. O mesmo trabalha com a madeira já cerrada em tábuas e pranchas, nas quais faz apenas o acabamento. Esta conversa teve grande importância, para o trabalho, pois contribuiu com mais um método de cubagem, chamado método popular. 
Nesse modelo, assim como no anterior, a tora é transformada em um paralelepípedo. Porém, através da divisão da circunferência média em 4 partes que passarão a ser largura e altura do mesmo. 
Assim: 

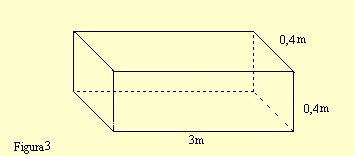
Comprimento da circunferência média=1,60m 
1,60m / 4 = 0,4m 

V= 0,4 x 0,4 x.3
V= 0,48 m³ 
Logo, modelo matemático 2 será: 
V= (Cm / 4 )2 . L onde Cm é a medida do comprimento da circunferência média, e L o comprimento da tora. 

3º) MODELO DO CILINDRO 

sse é o modelo que consiste em transformar o tronco ou tora em um cilindro. Para determinar o volume de um cilindro multiplica-se a área da base (círculo) pelo comprimento, e para tal utiliza-se como raio da base do cone, obtido a partir do diâmetro médio, ou da circunferência média.
Assim o modelo matemático 3 e dado por: 
V = π x r2 x h , onde a medida do raio médio da tora e h a medida co comprimento da tora.

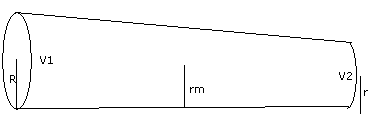
Figura4

V = 3,14 x (0,255)2 x 3
V = 0,612 m³ 
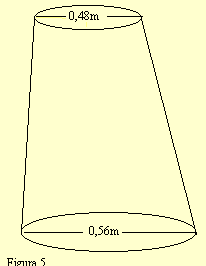
4º) MODELO DO TRONCO DE CONE 
Neste modelo, se compararmos a outro não há tanta perda, pois, suas medidas são usadas inteiras, ou seja, não é feita média nenhuma. 

Modelo do tronco de cone: 

onde h é a medida da altura, R a medida do raio maior e r a medida do raio menor . 

V=3,14 x (3/3)x(0,282+0,28*0,24+0,242) 
V = 0,638048 m³

PROBLEMA 2: O VOLUME DE UM TRONCO DE CONE PODE SER CALCULADO PELO VOLUME DO CILINDRO? 

Algumas coisas ficam óbvias sobre a questão, porém, matematicamente não é possível somente supor, e sim provar numérica e principalmente genericamente. Vejamos então a suposição e dedução abaixo: 
Volume do cilindro ≠ Volume do tronco do cone 

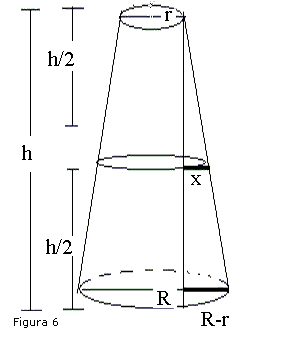
, onde Rm é o raio médio, matematicamente comprovado. 

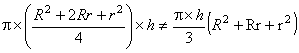
para vários valores de r e R.

 
Com isso, comprovaremos a veracidade da relação (I) 
Para provar que as fórmulas não são idênticas, uma forma e encontrar um exemplo onde se pode verificar a diferença. Utilizando o exemplo das medidas da tora temos:

V_cilindro = 3,14x(0,28+0,24)2x3 =0,636792;

V_{tronco de cone}=(3,14x3)x(0,282+0,28 x0,24+ 0,242)= 0,638048

0,636792<0,638048 

Verificou-se significativa diferença tanto nos cálculos numéricos anteriores bem como na demonstração genérica. Pode-se concluir que, o volume calculado pela fórmula do cilindro é diferente do volume obtido através da fórmula do tronco de cone. Isso se dá pelo fato de que ao transformar o tronco de cone num cilindro há uma perda na extremidade do raio maior e um ganho na extremidade do raio menor. Porém, nada nos garante que essas perdas e ganhos são exatamente ou somente razoavelmente compensatórios em relação aos diâmetros. Já no tronco de cone usamos as medidas das extremidades do tronco, já deixando de perder ao encontrar um raio médio como anteriormente. Sendo assim, consideramos o tronco de cone o método mais exato. 

PROBLEMA DA DIVISÃO DA TORA

 
Durante a entrevista com o madeireiro, ele mencionou que efetua a medição da madeira após o corte das toras em 6 metros, porque facilita o carregamento e também proporciona ao vendedor um maior rendimento da toras em termos de volume, pois se efetuasse o cálculo pelo seu método com as toras inteiras estaria proporcionando – se a si.  Efetuando-se então, a cubagem da mesma tora anterior, porém agora dividida ao meio para verificar a veracidade ou não da afirmação feita pelo madeireiro. Determinou-se então um novo diâmetro médio para as toras em questão.Fazendo a média entre os diâmetros encontrados através da medição dos volumes separadamente, conforme mostra o desenho abaixo. 

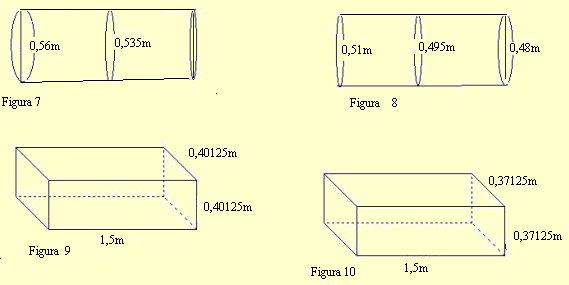
V1=0,241502 m³ V2=0,206734 m³ 
VT = 0,448236 m³ 

Comparando os resultados encontrados pelo madeireiro nos diferentes procedimentos verificamos que realmente calculando o volume da tora inteira ( V= 0,43892 m³) resulta num volume menor do que se calculando após a divisão das mesmas (V=0,448236 m³ ), obtendo assim uma diferença de 0,009316 m³. 
Depois ainda comparamos os resultados pelo cálculo do volume do tronco de cone, que, pelas conclusões anteriores julgamos mais aproximado (ou correto). 

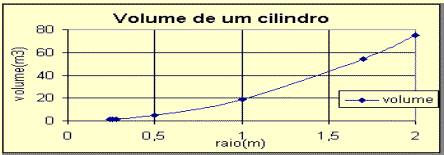
R= 0,28 m 
r = 0,255 m 

V1=0,33727525

R=0,255 m
r = 0,24 m 

VT = V1 + V2 

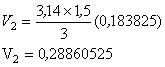
VT = 0,6258805 

Comparando – se os valores obtidos através do cálculo pela formula do volume do tronco de cone, obtivemos ainda pequena diferença de 0,0121675 m³, o que matematicamente não deveria acontecer, pois dividindo o tronco de cone imaginariamente ao meio não estaremos alterando o volume do mesmo. Concluímos, que tal diferença se deu devido à perda de casas decimais ou arredondamentos durante os cálculos. Por isso, decidiu-se desenvolver genericamente este cálculo para comprovar a igualdade. Usando novamente a dedução de Raio Médio (Rm), faremos a demonstração da igualdade do volume total (VT) e o volume calculado em partes (V1 e V2).
VT= V1 + V2 

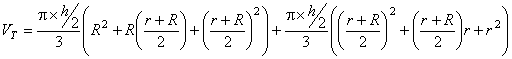
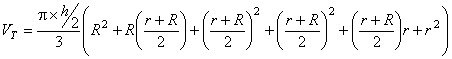
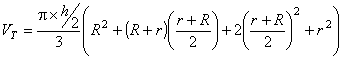
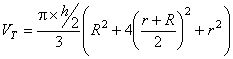
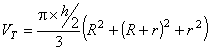
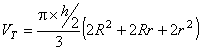
Verifica-se através da comprovação acima o afirmado anteriormente sobre a igualdade dos volumes, na divisão ou não da tora. 

3 - CONTEÚDOS DE MATEMÁTICA ENVOLVIDOS NA MODELAGEM DOS PROBLEMAS 

ATIVIDADES: 

1) Circunferência 
Usando varias latinhas de diâmetros diferentes , medindo-os e depois através destas medidas encontrar o valor da circunferência , pela formula C=π . D.Depois comparam-se os valores obtidos com as medidas das circunferências . 
Propor problemas para calcular os valores das circunferências, conhecendo-se os diâmetros e vice-versa. 
2) Paralelepípedo 
Utilizando caixinhas de diferentes tamanhos calcular seus volumes, planificar e calcular sua área. 
Criar situações-problema envolvendo diferentes medidas. 
3) Cilindro 
Utilizando latinhas de diferentes tamanhos comparar os volumes. 

ATIVIDADES DE ENSINO: 

1) Variando-se os valores dos raios nas formulas de calculo de volume do cilindro e de tronco de cone observa-se às diferenças entre os volumes obtidos ,tendo assim menor ou maior perda .

Altura	Raio menor	Raio maior	Volume cilindro	Volume tronco de cone	Diferença
5	2	4	141,3	146,44	5,14
5	2	6	251,2	271,96	20,76
5	1	4	98,12	109,83	11,71

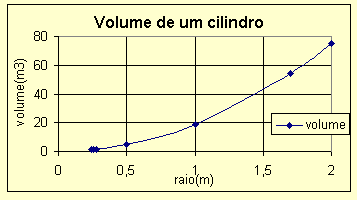
2) Utizando a fórmula do volume do cilindro V = π . r² . h , e considerando r variável e h constante, obtemos uma equação do 2º Grau. Atribuindo diversos valores para r, obtemos dados que colocados no gráfico forma uma parábola. A partir disto, o aluno estará trabalhando com equações e análises de gráficos.

Raio(m)	Volume
0,240	1,085184
0,255	1,225071
0,280	1,477056
0,500	4,71
1,000	18,84
1,700	54,4476
2,000	75,36

 

4 - CONCLUSÃO

Após a realização deste trabalho que objetivou pesquisar as diferentes formas de cubagem de madeira, bem como estabelecer relações entre elas, conclui-se que é de suma importância possibilitar aos alunos meios para que entrem em contato com estes diferentes métodos, principalmente, com aqueles mais usados quotidianamente. Considerando a valorização do que, muitas vezes, eles já viram, será uma motivação para os estudos dos métodos matemáticos formais.  Esta situação torna-se ainda mais significativa em nossa região, visto que no Noroeste do RS, ainda resta boa área de mata nativa, áreas com reflorestamento e muitas pessoas trabalham na cubagem de madeira, o que com certeza, seria diferente se fosse considerado o ensino em regiões muito desmatadas. 
Outrossim, destaca-se que os problemas analisados sob as diferentes maneiras de se realizar a cubagem possibilitou a constatação de que há semelhanças entre elas, mas algumas mais próximas e outras menos.  

Desta forma, verificamos a importância deste tema para nós professores, pelas diversas abordagens matemáticas e interdisciplinares que podem ser feitas em sala de aula e assim contribuir para formação de cidadãos críticos. Para tal, é um trabalho que não se propõe ser algo pronto, acabado e sim uma fonte de pesquisa e quem sabe estímulo de futuros estudos nessa área. 

Página elaborada na disciplina de Matemática Computacional IV – primeiro semestre de 2002


Adriana Mossmann, Alice Miranda, Janice Maldaner, Mara Bronstrup.