A Modelagem Matemática, a Estatística e a Informática estão presentes em muitas situações do cotidiano. Nesse contexto os jovens interagem através de varias experiências e informações, as quais os auxiliam na construção do conhecimento. Daí as necessidades educacionais de trabalharmos os conteúdos que integram os componentes curriculares, reafirmando-a como uma ciência presente no dia-a-dia, permitindo aos alunos uma melhor compreensão do mundo em que vivem.

Neste contexto, apresentamos um material destinado às atividades presenciais e a distância do curso Capacitação de Professores de Matemática do Ensino Médio. O material está estruturado em quatro partes. Na primeira parte apresentamos o texto Desenvolvimento de Currículo e Formação de Professores de Ciências da Natureza, Matemática e suas Tecnologias que trata sobre os pressupostos teóricos de uma Situação de Estudo(SE) seguido pela descrição das atividades relacionadas, de forma mais implícita a SE. Vale ressaltar que o referido texto é comum às áreas de Matemática, Física, Biologia e Química. Na segunda parte apresentamos o material para o desenvolvimento do tema Informática no Ensino da Matemática. De forma similar, na terceira apresentamos a Modelagem Matemática e na quarta parte apresentamos a Estatística. Estas são contempladas com questões teóricas e situações práticas, fundamentadas teoricamente nas situações de estudo.

Pensamos, ao elaborar o presente instrumento e no desenvolvimento do curso, promover o debate e a reflexão sobre questões pertinentes ao ensino da Matemática, contribuído com alternativas que permitam uma prática pedagógica que considere atividades que promovam o desenvolvimento de habilidades e competências pelo aluno.

As informações sobre as ferramentas e as formas de interação, entre os participantes do curso durante as atividades à distância estão em Anexo.

“A educação é um ato de amor e, portanto, um ato de coragem. Não pode temer o debate, a análise da realidade; não pode fugir à discussão criadora, sob pena de ser uma farsa”

Paulo Freire

Desenvolvimento de Currículo e Formação de Professores de Ciências da Natureza, Matemática e suas Tecnologias ^[1]

Dr Otavio Aloísio Maldaner

A Pesquisa Educacional desenvolvida nos anos 70/80, com forte ênfase em Teorias Construtivistas deixou, entre outras, duas lições importantes: 1.os alunos chegam à escola com muitas idéias e explicações acerca dos fenômenos naturais e do funcionamento dos produtos tecnológicos com os quais convivem em seu dia-a-dia e 2. essas idéias e explicações desempenham importante papel na aprendizagem das Ciências desenvolvidas na escola, por isso não podem ser desconsideradas nas propostas pedagógicas.

Sob diversas denominações – idéias prévias, idéias pré-científicas, idéias alternativas, conceitos espontâneos, conceitos do cotidiano, conhecimentos prévios, conceitos errôneos - essas idéias foram intensamente investigadas sob o ponto de vista de sua natureza e estrutura psicológica, origem e conservação, condições de mudança, interação com as idéias científicas, etc. Alguns modelos pedagógicos foram desenvolvidos, considerando sempre o papel ativo do aluno no processo, com participação maior ou menor do professor, com preocupação maior ou menor de suplantar as idéias anteriores para que as idéias científicas pudessem prevalecer. A continuidade da pesquisa revelou, ainda, que as pessoas podem conviver com diferentes modelos de explicação, incluindo os modelos científicos, utilizando-os conforme o contexto em que estavam envolvidos, conforme Mortimer (2000)[2].

Tendências pedagógicas atuais voltam-se mais para a compreensão do processo de formação das idéias e de constituição da mente das pessoas em seu meio social mais amplo ou na escola. Isso poderá levar a uma intervenção pedagógica mais eficaz no sentido da reconstrução cultural ampla junto às crianças e jovens em contexto escolar. Os conhecimentos prévios dos estudantes passam a ser vistos como formas internalizadas das vivências culturais significadas no meio social em que se encontram e não mais como construções espontâneas equivocadas. Os significados são produzidos na interação social e vão constituir a própria mente dos sujeitos. Isso ocorre em qualquer meio cultural. Os significados já internalizados estarão mais próximos ou mais distantes daqueles que a escola vai valorizar, o que ajuda a explicar o fato de uma criança “dar-se bem” ou “dar-se mal” na escola. Ao valorizar a cultura dominante, desconsiderando as outras formas culturais ricas e plenas de significados, as crianças e adolescentes das classes populares são consideradas incapazes, quando, na verdade, são as valorizações culturais diferenciadas que criam os desníveis. Ou seja, se a escola valoriza apenas as formas culturais dominantes gera a exclusão escolar e social pela reprovação.

No meio cultural contemporâneo, impregnado de artefatos tecnológicos só possíveis pela produção da Ciência, a maioria das pessoas desconhece os princípios científicos mais elementares. Os seus significados simplesmente não fazem parte da mente das pessoas, mesmo que tenham freqüentado a escola. Todos os levantamentos realizados nesse sentido mostram que os sujeitos sociais não especializados em uma área científica, mesmo com formação universitária, desconhecem princípios básicos de Física, Biologia, Química, Geologia, bem como, a base de funcionamento de equipamentos que utilizam. Isto é, as pessoas não foram constituídas nos significados dos conceitos da Ciência, embora seja propósito da escola fazê-lo na formação básica. Os mesmos levantamentos mostram que as pessoas que passaram por toda essa formação consideram que foi perda de tempo os estudos que fizeram dessas disciplinas e confessam que não aprenderam nada ou que não lembram nada.

É pensamento de Vigotski (2001)[3], e de outros teóricos da abordagem histórico-cultural, que a aprendizagem e a reconstrução cultural só ocorrem nas interações sociais. Os significados científicos parecem estar ausentes do meio social no cotidiano das pessoas, por isso não há transação significativa de significados, assim as idéias científicas não constituem os sujeitos. Este é um paradoxo, pois admite-se que vivemos a era científica, a cultura científica, o domínio tecnológico com base na Ciência, mas as pessoas não conseguem pensar na forma da Ciência sobre o mundo que vivem. Ao contrário, proliferam sempre mais outras formas não científicas de enxergar e interpretar os fenômenos naturais, sociais e psicológicos, mais assentadas em crenças do que na racionalidade humana científica construída historicamente.

Nesse contexto temos de refletir melhor o papel da escola na constituição dos sujeitos sociais. Cabe a ela o papel social de constituir os sujeitos nas outras formas culturais que determinado momento histórico exige. Para isso há uma forma escolar de produzir aprendizagem e desenvolvimento mental que deve fazer parte dos saberes específicos dos pedagogos de todos os campos do conhecimento humano, entre eles o campo científico. A compreensão de como se deve proceder para que a intervenção pedagógica seja eficaz, isto é, os estudantes se constituam nos conhecimentos científicos e desenvolvam a sua capacidade mental para um meio social com características específicas, muda historicamente. Admitimos, hoje, que os estudantes chegam à escola com explicações próprias sobre os fenômenos do cotidiano. Como operações mentais, elas são sustentadas por conceitos, cujos significados foram produzidos nas interações sociais, constituindo a estrutura mental. Não importa que esses conceitos (do cotidiano) sejam muito diferentes dos conceitos (científicos) que a escola precisa ensinar, eles são importantes no trabalho pedagógico, pois ambos serão enriquecidos mutuamente nesse trabalho, conforme defende Vigotski.

Fora do contexto escolar as interações dão-se ao natural, de forma assistemática, geralmente, diante de uma situação concreta do cotidiano das pessoas. Assim acontecem a aprendizagem e o desenvolvimento mediados pelos significados produzidos e internalizados diante da situação prática e em interação com outros sujeitos: adultos em interação com crianças ou crianças mais experientes em interação com outras crianças. Na escola, porém, há a intenção do ensinar e do aprender e o desenvolvimento mental dos estudantes é seu propósito. Temos, nessas duas situações, a mesma natureza humana, o mesmo sujeito, embora com outros propósitos. Não se muda a natureza humana só porque se está em outro espaço cultural! Isso nos dá os indícios de mudança nos procedimentos pedagógicos tradicionais nas salas de aula: produzir um ambiente rico em interações sobre determinada situação.

Ao aceitarmos a concepção histórico-cultural dos processos de conhecimento e de desenvolvimento da consciência e todas as faculdades mentais essencialmente humanas, estamos propondo uma nova prática pedagógica no processo de ensino e aprendizagem das disciplinas escolares, especialmente as disciplinas da área das Ciências da Natureza e suas Tecnologias no Ensino Médio. É nessa área que residem as maiores queixas dos estudantes e em que ocorrem os maiores problemas de aprendizagem e conseqüente reprovação escolar.

Como qualquer campo do conhecimento, as disciplinas escolares são constituídas de uma linguagem específica, de procedimentos peculiares e de um sistema de conceitos. Tudo isso é concretizado por um conjunto coerente de signos e instrumentos que precisam ser significados para que a posse do conhecimento pelos estudantes seja possível.

Propomos a Situação de Estudos como forma concreta de viabilizar o processo de gênese dos conceitos científicos na escola. É ela uma situação concreta, da vivência dos alunos, rica conceitualmente para diversos campos da ciência, de forma a permitir a análise interdisciplinar e transdisciplinar. A intenção é a de gerar conceitos científicos para os quais é essencial a organização, a coerência, a sistematização e intencionalidade para um novo nível de entendimento da situação, e isso constitui uma nova forma de conceituar, diferente da formação dos conceitos do cotidiano, pois o significado pretendido é do conhecimento de quem ensina desde o início e visado por ele (ela). Para isso, a Situação de Estudos eleita precisa apresentar múltiplas interfaces de interação, sempre mediada pela ação de outros e dos próprios conceitos que começam a ser significados, permitindo a reconstrução de uma totalidade no recorte feito no mundo real.

O indício da aprendizagem realizada estará, justamente, na capacidade de reconstrução da situação sob estudo na forma conceitual, passando a constituir a mente dos aprendentes com novas formas de raciocínio, de abstração e de representação do mundo. Na reconstrução teórica do real, os conceitos científicos se enriquecem de vivência, seus significados evoluem, enquanto os conceitos do cotidiano se reorganizam, caminhando para a abstração, despregando-se, sempre mais, da vivência.

Uma situação de estudo não deve ser um projeto demasiado audacioso, abrangente, interminável, mas deve ter um número relativamente pequeno de conceitos centrais iniciais, sendo estes sempre representativos do todo da disciplina, compondo uma totalidade para cada disciplina e do conjunto delas. Numa primeira situação de estudo, os conceitos terão apenas um entendimento inicial que deverá evoluir no decorrer do desenvolvimento de outras situações. É assim que os conceitos se constituem, conforme propõe Vigotski. Em primeiro contato com o conceito, pode ser que o significado produzido e internalizado, para determinado conceito, seja muito elementar. Em muitas outras situações este conceito deverá aparecer e, então, o seu significado poderá evoluir. Pode acontecer que de início o entendimento do conceito seja tão pequeno que se resuma a uma palavra com significado ainda difuso. Mas é importante que a palavra, representativa do conceito, esteja presente, seja usada na interação, os atores se detenham nela, discutam sentidos e significados que deverá ter em um contexto específico de uma disciplina ou no contexto inter e transdisciplinar. Ao evoluir o significado, o conceito passará a constituir a mente do aluno, permitindo pensar conceitualmente sobre a situação estudada ou sobre outras situações em que esse conceito se faça necessário.

A situação de estudo com as características acima traz a vivência anterior dos alunos para a sala de aula e permite que ela seja compreendida em novos níveis, mediado pela produção de significados na interação pedagógica, constituindo a consciência dos estudantes e permitindo que se desenvolva pela produção de conhecimentos impossíveis por vivência direta. A escola tem esse papel social de possibilitar uma compreensão mais ampla do mundo, refletindo conceitualmente sobre ele.

Pelo fato de uma situação de estudo partir da vivência dos alunos ela facilita a interação pedagógica necessária para que se produza conhecimento. Eventualmente ocorrerão passagens em que há alta vivência dos alunos que permitirá que participem intensamente dos debates, da elaboração e organização de dados, produzam idéias e as defendam. Além disso, as situações de vivência permitem que o objeto sobre o qual estudantes e professor estão se referindo seja comum sob o ponto de vista psicológico, o que faz com que os conceitos do cotidiano se façam presentes e passem a interagir com os conceitos científicos que serão introduzidos, permitindo que ambos evoluam para novos níveis, como dissemos acima.

Professores do Ensino Médio, mais ainda, do Ensino Superior, recebem alunos já bastante “escolarizados” no que se refere à busca e organização de informações com vistas à produção de conhecimentos. Por um desvio de concepção do processo ensino e aprendizagem, produzido historicamente no Brasil, os estudantes acabam enredados em uma prática pedagógica que os torna extremamente passivos no que se refere aos conteúdos escolares. Estão sempre no aguardo de copiar os resumos de matéria que os professores colocam no quadro de giz e por eles se guiam para os seus estudos com vistas às provas ou “avaliações”, conquistando a certificação do aprendido. Presenciamos nas salas de aula do nível médio e universitário verdadeiras cópias de conteúdos considerados prontos e aprendidos uma vez copiados e repetidos nas provas. Se, por acaso, um professor tenta romper esse esquema, iniciar uma discussão e deixar por conta dos alunos as anotações necessárias para um possível roteiro de estudos posteriores e/ou complementares, não fornecendo “apostilas”, os alunos ficam totalmente perdidos, rebelam-se contra essa situação e praticamente exigem que se volte ao esquema que conhecem, principalmente em disciplinas que julgam não serem essenciais para a sua formação profissional.

Não se trata de apontar culpados. Dissemos que esse processo foi produzido historicamente, portanto aceito e validado. Os menos culpados são os estudantes, pois coube a eles aceitar o processo e dentro dele foram acomodados. Nós educadores temos de saber onde e como romper o processo. O nosso grupo está propondo a situação de estudo no ensino médio como uma tentativa, também, desta ruptura, além de todas as vantagens apontadas acima. A aprendizagem vai se dar no próprio processo da interação, nos tempos e espaços da escola, e seu desenvolvimento mental vai se seguir, conforme a crença teórica que estamos adotando. Durante as aulas e após os alunos registram suas produções com base nas fontes de informações disponibilizadas e produzidas coletivamente. A avaliação muda, igualmente, pois cada aluno será estimulado a pensar sobre uma nova situação com o uso do esquema conceitual com o qual já foi constituído. A coerência do esquema e sua abrangência serão indícios da produção coletiva realizada, inclusive do trabalho do professor. O resultado permitirá redirecionar a situação de estudo para futuros trabalhos, sendo a principal fonte de pesquisa do professor sobre seu trabalho e de seu aperfeiçoamento.

Com a Lei de Diretrizes e Bases da Educação Nacional, as Orientações Curriculares para o Ensino Médio foram propostas na forma de Parâmetros, os Parâmetros Curriculares Nacionais, entre os quais os PCNEM (Parâmetros Nacionais do Ensino Médio). Nova versão foi produzida em 2005 e deverá circular em breve nas escolas. O grande desafio é, ainda, compreender o Ensino Médio como parte da Educação Básica e não mais com o sentido preparatório ou propedêutico para o ingresso na universidade. No Brasil, criou-se muito a cultura da preparação dos estudantes para a série seguinte, para o grau seguinte, isto é, fomos motivados a produzir educação que servisse ao sistema educacional, excluindo, pela reprovação e repetência, a todos aqueles que não atendiam a essa orientação. A Educação Básica até o Ensino Médio traz uma nova lógica, novas orientações e novas motivações.

Uma das críticas ao Ensino Médio é a sua forma excessivamente disciplinar - marcada pela total separação entre as disciplinas - e seu distanciamento das questões de tecnologia. Dentro das disciplinas, os conteúdos são desenvolvidos de forma fragmentada e linear e, em conseqüência disso, ocorre aprendizagem baixa qualidade e superficial, insuficiente para um bom desenvolvimento mental.

Estamos convencidos de que é possível desenvolver e implementar mudanças no currículo e na formação escolar (ensino médio) que possam romper com o satus quo das escolas viciosamente instituído e disseminado. As mudanças demandadas ao professor e à escola, hoje, requerem visões e práticas organizativas em novos patamares. Supõem a instituição de coletivos organizados que constituam processos de interação colaborativa, promovendo intervenções capazes de articular dinâmica e intencionalmente os espaços e a formação como um todo. É nesse sentido que colocamos em discussão a modalidade de organização curricular na forma de Situações de Estudo (SE).

O contexto de problematização de uma SE torna possível estabelecer espaços de negociação de significados aos conceitos introduzidos, o que permite o entendimento e a ação no contexto em novos níveis. Assim, articuladamente à exploração de uma SE, vão sendo inseridas abordagens disciplinares que, extrapolando seus âmbitos internos, assumem características inter e transdisciplinares.

A tematização de uma SE torna possível estabelecer interações e intermediações que constituem aprendizados de saberes inter-relacionais e inter-complementares, na constituição do saber escolar. Os conceitos são abordados em seus processos de construção histórica, em seus antecedentes, conseqüentes, relações e implicações com a vida na sociedade.

O contexto da SE torna possível que os alunos reflitam critica e conceitualmente sobre meio social, o que os capacita para a recriação desse meio, modificando-o e por isso modificando-se, à medida que são incentivados a aprender a aprender.

A situação de estudo, como uma forma organizada de ensino, explicita quais os conteúdos do ensino e como são trabalhados esses conteúdos. Abrange conceitos das diversas áreas, e também os diversos temas de relevância social, em atenção ao modo como esses componentes diversos se inter-relacionam e se inter-complementam entre si, na formação como um todo. São trazidos à tona vivências e aprendizados anteriores que participam dinamicamente nas abordagens e construções. Trata-se de contextos de interação, que abrangem interlocutores fisicamente presentes e ausentes, incluindo professores, colegas, especialistas, pessoas entrevistadas, palestrantes, autores de publicações diversificadas (livros, revistas, jornais, vídeos, internet, dentre outros).

Cabe a cada grupo explicitar, nessa nova modalidade de organização do ensino, os conteúdos conceituais, os procedimentos, as atitudes, os valores que permitam visualizar os aprendizados que vão sendo desenvolvidos ao longo da formação. Nesse sentido, foi proposto o que consideramos em 2000 um exercício coletivo dessa modalidade de organização do ensino através de SÉS, e que, de acordo com nosso pensamento, permite um trabalho com característica interdisciplinar, transdisciplinar e intercomplementar.

Ao propormos sucessivas SEs como nova organização curricular área científica estamos rompendo com práticas tradicionais de organização curricular, com base em disciplinas separadas e desenvolvidas de forma fragmentada e linear. Não vamos descrever como são essas formas, pois os professores de Biologia, Química e Física as conhecem muito bem e basta folhar os livros didáticos tradicionais para se saber do que estamos falando. Com a SE mantemos as disciplinas, organizadas, porém, para atender à análise, compreensão e entendimento, sob o ponto de vista das diferentes ciências (Biologia, Química, Biologia e outras), de uma determinada situação prática do mundo material. Em torno de uma situação eleita organiza-se uma equipe de professores, tentando explicitar entendimentos essenciais em torno dos conceitos que cada disciplina vai usar em sua análise, que serão intencionalmente explicitados junto aos alunos. Desejamos, com isso, ultrapassar a visão multidisciplinar da situação sob estudo e atingir a interdisciplinaridade e a transdisciplinaridade ou, mesmo, a intercomplementaridade de conceitos utilizados, bem como dos sistemas conceituais e das abordagens próprias de cada campo do conhecimento disciplinar.

Os profissionais de cada ciência e de cada disciplina têm a sua razão de ser. Atuam com um sistema consistente de conceitos, desenvolvem procedimentos e instrumentos próprios à abordagem de uma situação, prezam por um conjunto próprio de valores e desenvolvem atitudes e jargões que os identificam. Por isso constituem uma comunidade científica na qual reconhecem e validam as produções realizadas pelos diferentes membros que a compõem. As diferentes comunidades, também, interagem entre si de tal forma que avanços teóricos e técnicos produzidos em uma delas logo influenciam as outras.

Na formação básica é importante que os sujeitos se constituam nessa forma inter e transdisciplinar, tornando-os mais autônomos em relação ao meio social, tecnológico e natural, isto é, capazes de decidir e propor mudanças sobre situações práticas que, de alguma forma, produzam exclusão, injustiça, degradação ambiental e da qualidade de vida das pessoas. A constituição das pessoas nessa direção não é espontânea, precisa ser intencionalmente buscada. Não se pode esperar que cada sujeito, diante de múltiplas situações propostas em cada disciplina escolar, capacite-se a agir com competência e responsabilidade em seu meio. As situações do meio não permitem abordagens simplistas, parciais. Elas exigem capacitações interdisciplinares, compreensões amplas e transdisciplinares, muitas vezes, com o concurso multidisciplinar, isto é, vários profissionais atuando numa mesma direção, com o mesmo objetivo, o que é, também, uma capacidade desenvolvida na educação básica.

No desenvolvimento de uma SE, é importante que a questão epistemológica esteja presente. Esta se refere à produção de uma ciência e à sua validação. Contrariamente do que muitos crêem, a Ciência não se apoia nas aparências e nem busca essências escondidas na natureza. É, a Ciência, uma construção humana, portanto, histórica, que se dá com o desenvolvimento de conceitos ou idéias que se confrontam com os dados sensoriais e as convicções espontâneas. Insistimos, a produção dá-se no confronto de uma situação prática, pela compreensão conceitual do que está além das aparências e das impressões primeiras. Por isso, a situação experimental, a prática, a experimentação, jamais, deve ser esquecida na ação pedagógica. Ao contrário, deve-se confrontá-la com os conceitos já construídos historicamente, mostrar que não se pode “captar” pelos sentidos imediatos a existência, por exemplo, dos átomos, das funções das estruturas biológicas ou das leis de Newton. Pode-se, porém, à luz dos conceitos das diferentes ciências, entender essas mesmas realidades, atingir novo nível de compreensão, impossível pelos dados sensoriais ou pelas idéias primeiras. Uma vez de posse dos conceitos, através da interação pedagógica, os próprios dados sensoriais começam a ter novo sentido, nova compreensão. Com isso não queremos dizer que os dados sensoriais captam de forma errada as coisas, apenas que não captam as explicações que a Ciência dá para as sensações e percepções.

Para superar a concepção fragmentada que nós professores temos de nossa disciplina, propomos como ideal que em toda a SE tenhamos em mente a disciplina como um todo. Podemos ter em vista os conceitos mais centrais e não a seqüência linear dos conceitos tradicionais. Esses conceitos centrais vão retornar muitas vezes em outras situações de estudo, evoluindo seu significado. Esperamos, com isso, poder explicar cada situação dentro das diferentes disciplinas, até onde o nível conceitual vai permiti-lo. É assim que na Física, por exemplo, teremos presentes fenômenos elétricos e seus princípios teóricos desde o início, ao lado das leis de Newton e, também, das compreensões da Física Moderna, ou, ainda da compreensão inicial do conceito pressão ao abordar a pressão atmosférica através da energia cinética dos gases que compõem o ar.

A SE “Ar Atmosférico” foi o primeiro exercício coletivo desenvolvido pelo Gipec-Unijuí e em interação com os professores da Área das Ciências da Natureza e suas Tecnologias da Escola Francisco de Asses (EFA). Após o primeiro exercício, a SE foi desenvolvida várias vezes nas escolas e acompanhada por diversas pesquisas nos mais diversos enfoques. Até hoje é considerada adequada para introduzir os estudantes do Ensino Médio no estudo da Física, Química e Biologia com área de estudo. Ela é desenvolvida com a finalidade de compreender uma importante porção do mundo material que é o ar atmosférico e a relação que tem com o fenômeno vida. Objetiva-se produzir uma visão global, uma totalidade, olhando sua origem (Geologia), sua dinâmica e permanência (Física), sua composição e transformações (Química), sua relação com os seres vivos (Biologia) e as relações práticas que o ser humano estabelece com esse meio gasoso que o cerca e o impregna (Tecnologias, Poluição Atmosférica).

Em sua forma original, as SEs no Ensino Médio, foram concebidas e configuradas na forma de um hipertexto, com diversas possibilidades de entrada de assuntos relacionados à situação, com a explicitação de conceitos, explicações adicionais, informações, novas fontes de informações, etc., abrangendo as diversas disciplinas do currículo. Essa modalidade exige a organização dos professores com tempos e espaços para planejamentos coletivos, ao menos uma hora por semana. Para cada SE deve ser escolhida uma disciplina que faz a narrativa, mantém a lógica. As outras buscam contribuir para o entendimento da situação em aspectos que a primeira disciplina não dá conta. A escolha da disciplina depende da lógica com que se deseja abordar a situação sob estudo. Se for sob a ótica de temáticas dentro de uma situação mais ampla, não há a necessidade de escolher uma disciplina que faça a narrativa central. Até aqui, a SE Ar Atmosférico teve como narrativa a Química, mas no presente trabalho optou-se por temáticas, desaparecendo a figura “disciplina narrativa”.

O ar atmosférico é normalmente definido, em livros didáticos de Ciências, como uma fina camada gasosa que circunda a superfície terrestre. Embora se encontrem partículas de ar em distâncias acima de 400 quilômetros (km) da superfície (exosfera), região em que orbitam os satélites artificiais, 90% das partículas do ar estão contidos nos primeiros 16 km da superfície ou de altura. A idéia de “fina camada” é relativa ao diâmetro da terra, de aproximadamente 12.000 km. A camada não é uniforme, mudando de características gradualmente com a altura ou a distância da superfície terrestre a partir do nível do mar (altura zero). Muda, principalmente, a concentração de ar, que podemos chamar como o número de partículas dos componentes do ar por volume. Criou-se uma sistematização em camadas para fins de estudos, descrevendo características salientes de cada camada atmosférica. Um modelo representativo do planeta como um todo, feito em escala, dá uma idéia de grandeza relativa daquilo que chamamos atmosfera terrestre. Esta é uma atividade que pode ser proposta aos alunos, utilizando informações básicas sobre as diferentes camadas em que se costuma dividir a atmosfera (troposfera, estratosfera, mesosfera, termosfera, exosfera). Dizemos, então, que a distribuição do ar na atmosfera não é homogênea, embora uma pequena porção de ar possa ser considerada uma mistura homogênea. Os intervalos de altura para cada camada não são rígidos, podendo ser propostos até 11 km para a troposfera, 11-35 km para a estratosfera, 35-80 km para a mesosfera, 80-400 km para a termosfera e acima de 400 km temos a exosfera. Sobre essa porção material desejamos produzir entendimentos sob o ponto de vista das Ciências da Natureza, significando conceitos centrais das disciplinas que compõem a área.

INFORMÁTICA NO ENSINO DA MATEMÁTICA

Tânia Michel Pereira[4]

Endereços: R. José Ceretta, 170-Ap.303, Bairro São Geraldo, Ijuí –RS Cep 98700-000

tmichel@unijui.tche.br

Fones: 55 3332 7794-Residencial ou 55 3332 0278
Página: http://www.projetos.unijui.edu.br/matematica/tania

Nos últimos anos, com a popularidade da internet os computadores individuais deixaram de ter status de máquinas poderosas e se transformaram em componentes da informática. O tempo de discutir se o computador deve entrar na escola também já passou. O fato é que muitas escolas estão equipadas com laboratórios de informática com vários computadores interligados e muitos destes ligados à internet. Em várias escolas do Estado do Rio Grande do Sul os primeiros computadores a entrar nas escolas foram comprados por associações que envolvem pais, professores e alunos. Isto evidencia o interesse destes três segmentos da comunidade escolar na utilização de computadores no processo ensino aprendizagem nas escolas. A dúvida que permanece é como potencializar o uso da informática nas áreas específicas?

O interesse dos jovens pela informática é também um fato consumado, principalmente quando se trata de internet. Pesquisa escolar é sinônimo de pesquisa na internet, para os jovens com acesso à esta. A cada dia, a internet agrega mais pessoas, principalmente jovens. Por outro lado, é percebível que a proporção de jovens interessados em aprender matemática, na sala de aula convencional, está reduzindo nos últimos anos. Os navegadores Web estão agregando novas funcionalidades, aumentando as possibilidades de produção de materiais didáticos, com bons efeitos visuais. Considerando estes fatos pode-se perguntar, porque não utilizar o potencial de recursos oferecidos pela informática, relacionados com a tecnologia Web para criar ambientes de aprendizagem que podem ser acessados via internet ou com as características idênticas a esta?

Pesquisas em Educação Matemática tem revelado que, o uso da informática funciona muito bem, como elemento motivador no processo ensino e aprendizagem de matemática. Isto pode parecer pouco. Mas, ter alunos interessados em aprender é fundamental para que o processo ensino/aprendizagem se efetive, pois é uma das condições necessárias para tal.

Para aprimorar as metodologias de ensino neste curso serão analisados e construídos materiais didáticos virtuais que envolvem as novas tecnologias de informação. Os programas computacionais que serão utilizados durante as aulas de Informática no Ensino da Matemática envolvem navegadores de internet, editores para compor páginas para internet, planilha eletrônica, aplicativos específicos para matemática com computação algébrica, numérica e gráfica. A seguir serão apresentadas as atividades que serão realizadas durante o estudo do tema Informática no Ensino da Matemática. Além disto, a apresentação, o reconhecimento, simulações e a primeira utilização do Ambiente EaD específico do Curso, será efetivado durante o desenvolvimento deste tema.

Reconhecimento do Ambiente EaD do Curso

Objetivo:

Conhecer o Ambiente Específico do Curso.

O ambiente poderá se acessado no seguinte endereço:

http://www.projetos.unijui.edu.br/matematica/tania Neste ambiente você pode trocar mensagens on-line com a secretaria do DeFEM - Departamento de Física, Estatística e Matemática, para isto clique no link “Estamos on-line” ou deixar uma mensagem, caso apareça o link “Deixe seu recado”. As páginas individuais com a sua foto e os trabalhos realizados durante o curso presencial também serão colocadas neste ambiente, para fins de socialização entre os colegas do curso. Na opção mensagens você poderá enviar mensagens para seus colegas. No bate-papo você poderá trocar mensagens instantâneas com seus colegas desde que seja combinado um horário específico para tal. Na opção Fórum você pode contribuir na discussão sobre temas específicos tais como: Informática, Modelagem Matemática, Estatística ou Situação de Estudo no Ensino Médio. A maior parte do que você encontra no ambiente será fornecido aos participantes do curso num CD. Neste CD você encontrará todo o material do site “Material Didático para Matemática na Educação Básica e Ensino Superior” do endereço http://www.projetos.unijui.edu.br/matematica/ entre outros utilitários.

ATIVIDADE I

Seminários Situação de Estudo

Objetivo:

-Vivenciar uma pesquisa na internet orientada para o ensino da matemática relacionada a situação de estudo Ar Atmosférico.

A situação de estudo permeia todo o curso e inicia com a primeira palestra, onde será apresentado o desenvolvimento da Situação de Estudo: “Ar atmosférico”. Palestra é proferida para todos com os professores do curso de capacitação que envolve professores de Química, Biologia, Física e Matemática.

1.1 Pesquisas na internet orientadas para a situação de estudo Ar Atmosférico

Nesta atividade cada dupla receberá uma lista de endereços pré-selecionados para iniciar a pesquisa na internet. Para cada endereço deverão ser copiados os seguintes dados para posterior análise: endereço do Site; autores do texto e os textos que contém dados que interessam.

1.2 Elaboração de atividades de matemática envolvendo a situação de estudo Ar Atmosférico

A partir das informações obtidas e a turma organizada em grupos serão propostas atividades de matemática que podem contribuir para o aprofundamento do tema em questão, bem como para propor tópicos de matemática que podem ser aprofundados a partir da motivação ou necessidade que a situação de estudo pode provocar. As atividades propostas pelos grupos serão digitadas num editor HTML da ATIVIDADE II deste curso, servindo como o primeiro exemplo de prática de construção de páginas para fins didáticos.

1.3 Atividades à distância envolvendo situação de estudo

Durante as atividades à distância cada professor, em sua escola, deverá produzir atividades relacionadas á uma nova situação de estudo junto aos professores e/ou alunos do Ensino Médio, na disciplina de Matemática. A descrição da SE e as atividades de matemática elaboradas na escola, relacionadas a situação de estudo em questão, deverão ser apresentadas em formato HTML em disquete ou CD da segunda etapa presencial.

O atendimento On-line para Situação de Estudo para as turmas A, B e C será dia 25/04/2006 no turno da tarde das 13h:30mim até 17h:30min no endereço http://www.projetos.unijui.edu.br/gipec. Para mensagens o endereço para o acesso pode ser: http://www.projetos.unijui.edu.br/matematica/tania para possibilitar o retorno das mensagens neste último endereço, é necessário o fornecimento do e-mail de quem enviou a mensagem.

ATIVIDADE II

2- Editoração de páginas para internet a partir de um bloco de notas

Objetivos:

-Conhecer a estrutura da linguagem HTML e seus principais delimitadores.

-Construir páginas utilizando delimitadores do HTML.

Uma página escrita em HTML (Hiper Textos Markup Language) é um texto que pode ser escrito num bloco de notas ou em editores específicos para tal. Iniciaremos nosso estudo no bloco de notas para entender um pouco da estrutura desta linguagem.

Consideramos aqui o sistema operacional Windows da Microsoft. A escolha se foi baseada no fato de que, existem muitos usuários com este sistema operacional e além disto, esta atividade é presencial e com possibilidade de utilização em qualquer um dos laboratórios da UNIJUÍ, local onde serão desenvolvidas as aulas presenciais.

2.1 Abrindo o bloco de notas

O bloco de notas, que normalmente pode ser aberto pelo seguinte caminho:

-> -> ->.

As vezes este se encontra dentro de alguma pasta dentro de Acessórios. Neste caso é preciso procurar o programa desejado com ajuda do mouse.

O bloco de notas normalmente é similar a figura a seguir

Seguiremos um modelo de estrutura bem simples. E vamos digitar o que está sendo mostrado na figura a seguir no bloco de notas que você abriu.

Observe que na primeira linha aparece <html> e na última aparece </html>. Acontece que na primeira linha abriu o marcador <html> e na última fechou este marcador contendo a barra da divisão antes da palavra html e ambas aparecem entre os sinais < e >. Isto pode ser comparado na linguagem matemática com abre chaves e fecha chaves. Uma Página com HTML puro, sempre abre e fecha desta forma. Observe agora os delimitadores contendo <head> (cabeçalho interna) abrem e fecham entre dos delimitadores <html> e </html>, como se acontece com colchetes, na linguagem matemática e além disto entre os delimitadores que abrem e fecham <head> encontramos outro marcador <title>(título interno) que abre e fecha, dentro dos head, justamente como acontece com os parênteses dentro dos colchetes na nossa analogia. Os delimitadores <body> e </body> delimitam o texto que efetivamente irá aparecer na página.

Agora vamos criar uma pasta para colocar todas as páginas que você era compor. Isto pode ser feito conforme passos a seguir:

2.3 Criando uma pasta

Crie uma pasta na área de trabalho e nomeie-a com o teu nome. Isto pode ser feito do modo como descrevemos a seguir.

Minimize o bloco de notas clicando no botão com um sinal de menos que fica próximo à extremidade superior direito da janela do bloco de notas.

Na área de trabalho, com o mouse, escolha um local que não esteja ocupado com outro arquivo ou pasta. Clique no botão direito do mouse, e na janela que abre escolha Novo, e dentro das opções que aparecem escolha Pasta. Assim que a pasta aparecer na área de trabalho, digite teu nome ou de um dos componentes do grupo, utilizando somente letras minúsculas, em vez de espaço utiliza sublinhado e não coloque acentos nem cedilha.

Nesta pasta serão gravados todas as páginas construídas nesta etapa do curso. O conteúdo do bloco de notas deve ser salvo para que possa ser interpretado por um navegador de internet e visualizado como página da internet.

2.4 Salvando a página

Salve a página que você digitou e minimizou dentro da pasta recém criada. Você pode fazer isto do modo descrito a seguir.

Para salvar o conteúdo da página em HTML digitado num bloco de notas, clique em -> . Na janela que abre, siga os passos que aparecem na próxima figura.

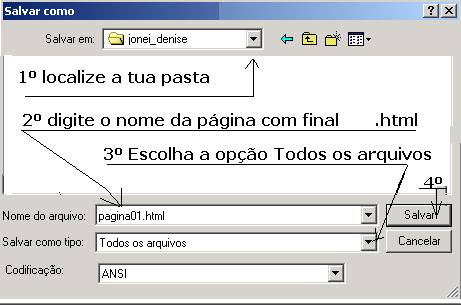
É importante que o material que está sendo digitado seja salvo periodicamente num intervalo não superior a 30 minutos, para que não se perca muito do que foi digitado, no caso de algum imprevisto, como uma oscilação brusca de energia. Nas próximas vezes em que este mesmo arquivo for salvo, basta clicar em Salvar em vez de Salvar como.

Depois que você salvou a página com o nome pagina01.html, abra a pasta que você criou e salvou sua página, dê um duplo clique sobre a sua página e veja como ela aparece. Ative novamente o bloco de notas, clicando sobre o mesmo, este deve estar aparecendo na barra que fica na parte inferior da tela do computador. Clique nele para ativa-lo.

Dentro da página que foi aberta com o bloco de notas, coloque o seu nome completo, em português correto entre os marcadores <title> e </title>. Altere também a frase “Aqui você deve digitar seu texto”, caso este se encontre entre os marcadores <body> e </body>. Salve novamente a página clicando somente em Salvar, que á uma opção do menu que aparece ao clicar em Arquivo. Clique novamente sobre o arquivo dentro da pasta para ver como está sua página agora. Veja se aparece o seu nome ou os nomes do grupo na barra superior azul da página.

Neste momento iremos nos preparar para iniciar a composição da página para expor as atividades de matemática elaboradas em grupo na ATIVIDADE I. deste instrumento. Antes disto, vamos conhecer mais algumas informações necessárias para elaboração de um texto em HTML com o bloco de notas.

Você deve lembrar que todo o conteúdo texto deve ser digitado logo após a abertura do marcador <body> e antes de </body>, ou seja entre os marcadores <body> e </body>.

2.5 Marcadores e delimitadores principais dentro de um texto

Marcador de nova linha ou 

Quando você quiser uma nova linha dentro do texto, não basta acionar a tecla Enter. Este modo de conseguir uma nova linha só funcionará na parte interna. Para que a nova linha apareça você pode colocar o marcador de nova linha . Este marcador não é delimitador, é só uma marca de nova linha.

Delimitadores de parágrafo 

Se você quiser um espaço duplo entre os parágrafos do texto é preciso iniciar o parágrafo com o delimitador e fechar o parágrafo com o delimitador

Delimitador de sobre-escritos e subscritos

Para sobre-escritos utilize expoente e para subscritos índice . Por exemplo, para que apareça 5² digita-se 5 2 e para que apareça x₃ digita-se x 3.

Está na hora de construir a página com as atividade relacionadas ao Ar atmosférico!

Com as informações até aqui colocadas você pode compor a página das atividades criadas por você na ATIVIDADE I. deste documento. Se você necessitar outros recursos procure-os nas informações que seguem abaixo.

2.6 Outros Informações sobre HTML

Apresentamos a seguir outras informações sobre a linguagem html que servirão de subsídios para formatos especiais que você queira utilizar em pagina para melhorar a estética da mesma.

Delimitador de recuo do texto <blockquote> Texto </blockquote>

Delimitador de Itálico O texto em itálico

Delimitador de texto centralizado <center>texto centralizado </center>

Delimitador de texto sublinhado texto sublinhado

Delimitador de texto negrito texto negrito

Delimitador de comentários internos <! -- comentários interno não aparece na tela -->

Espaço em branco

Alinhamento do texto

<center> Texto centralizado </center>

 Texto centralizado

 Texto alinhado à direita

 Texto alinhado à esquerda 

 Texto justificado 

Escolhendo a cor da letra

Texto com letra verde

Texto com letra azul

Texto com letra grafite

Texto com letra vermelha

Escolhendo a cor do fundo

Altere <body>para <body bgcolor="#CCFFCC"> para cor de fundo verde

Altere <body> para <body bgcolor="#FFFFCC"> para cor de fundo amarela

Altere <body>para <body bgcolor="#CCCCCC"> para cor de fundo cinza

Altere <body> para <body bgcolor="#CCFFFF"> para cor de fundo azul

Altere <body>para <body bgcolor="#99CC99"> para cor de fundo verde

Criando Tabelas

<table> começo da tabela

<tr> começo da primeira linha

<td> começo da primeira coluna

é aqui que deve ser colocado o texto ou valor da primeira coluna da primeira linha

</td> fim da primeira coluna

<td> começo da segunda coluna

é aqui que deve ser colocado o texto ou valor da segunda coluna da primeira linha

</td> fim da segunda coluna

</tr> fim da primeira linha

<tr> começo da segunda linha

<td> começo da primeira coluna

é aqui que deve ser colocado o texto ou valor da primeira coluna da segunda linha

</td> fim da primeira coluna

<td> começo da segunda coluna

é aqui que deve ser colocado o texto ou valor da segunda coluna da segunda linha

</td> fim da segunda coluna

</tr> fim da segunda linha

</table> fim da tabela

Inserindo figuras

Inserir foto <img border="0" src="maria_da_graca_galvao.jpg" >

Inserir figura <img border="0" src="vierem.gif" >

Inserir figura <img border="0" src="unijui.bmp" >

Observação: as figuras ou fotos que serão inseridas desta forma deverão ser colocadas na mesma pasta da página que a chama.

Inserindo Links

Link para internet <a href=" http://www.projetos.unijui.edu.br/matematica">Laboratório virtual de Informática</a>

Link para uma página da mesma pasta <a href="pagina2.html">Segunda parte</a>

Link para uma página da pasta interna testes <a href="testes/pagina2.html">Página Pessoal de Maria da Graça Galvão</a>

Link para uma página da pasta anterior <a href="../index.html">Página inicial </a>

Letras gregas

α para obter α β para obter β δ para obter δ

ε para obter ε θ para obter θ λ para obter λ

π para obter π Ω para obter Ω Σ ara obter Σ

2.7 Transformação de um texto digitado no editor de textos Word para HTML

Um texto digitado do editor de texto Word pode ser transformado diretamente para HTML. Para isto basta salvar o referido texto do seguinte modo:

Clique em Arquivo-> Salvar como. Na janela que abre, siga a instrução da figura abaixo:

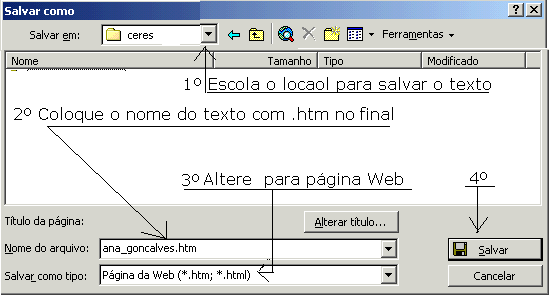
Se no documento digitado no Word tiverem figuras, fotos ou equações digitadas no editor de equações, será criada, de forma automática, uma pasta com as figuras separadas. O nome da pasta, para o exemplo da figura acima é Arquivos_ana_goncalves. Você pode utilizar este procedimento para reduzir figuras.

Para que esta página ana_goncalves.htm criada desta forma funcione, a pasta criada automaticamente deve estar acompanhada sempre ao “lado” da pasta Arquivos_ana_concalves. Caso contrário as figuras não aparecerão ao abrir a página.

ATIVIDADE III

3 Elaboração da página pessoal a partir de um modelo de página simples

Objetivos:

-Conhecer técnicas de tratamento de imagem para reduzir o seu tamanho em byte, utilizando o programa Paint, Word e bloco de notas.

-Praticar a elaboração de páginas com figuras

<html><head><title>Nome do professor </title> </head>

<body>

<h3 align="center">Ministério da Educação

Fundo Nacional de Desenvolvimento da Educação

Diretoria de Programas Especiais

Secretaria da Educação do Estado do Rio Grande do Sul

Universidade Regional do Noroeste do Estado do Rio Grande do Sul

Departamento de Física, Estatística e Matemática

Programa de Melhoria e Expansão do Ensino Médio

Curso de Capacitação dos Professores de Matemática do Ensino Médio

</h3>

Nome completo do professor

Coloque aqui um texto com a sua apresentação ao grupo colocando as seguintes informações: idade, estado civil, o número de filhos(se for o caso), sua formação, local de trabalho com endereço e telefone, seu e-mail, um telefone para contatos, seu endereço residencial, se tem computador em casa como está conectado à internt, o que gostas de fazer nas horas de folga, qual o seu sonho para o futuro número de alunos da escola, número de computadores da sua escola, série em que atua atualmente r outras informações que você considera importante.

</blockquote> </body> </html>

Para saber mais sobre construção de páginas pessoais, entre no endereço

http://b2.adm.idbrasil.org.br/usuarios/beneditomedeiros

3.1 Tratamento de fotos ou outras imagens

Para que sua foto digital ou uma outra figura elaborada no programa Paint, que você quiser utilizar para compor um material didático, apareça rápido na tela você pode proceder da seguinte maneira:

Clique sobre o arquivo que contém a figura, utilizando o lado direito do mouse. Entre as opções que aparecem escolha Abrir com , em seguida clique em Escolher programas. Ao abrir uma nova janela, procure entre as opções o programa Paint. Caso este não esteja na listagem, clique em outros e procure-o em disco C->Arquivo de programas->acessórios ->clique em Paint.

A sua figura ou foto deverá aparecer na área de trabalho do Paint. Clique em Editar-> Selecionar tudo, clique novamente em Editar -> Copiar.

Abra o editor de textos Word, clique em Editar ->Colar e salve o arquivo do Word com a(s) figura(s) como página Web conforme mostra a figura abaixo.

Estando o arquivo salvo, abra a pasta que inicia com Arquivos_. Neste local geralmente aparecerão as figuras mais “leves”. Isto depende muito da versão do Office instalado. Utilize estes procedimentos para reduzir o “peso” de sua foto em seguida copie as figura mais leves para a pasta onde sua página será gravada. Se você não souber como copiar um arquivo que pode conter figura ou texto e colar em outro local veja como fazer isto nos passos a seguir.

3.2 Copiando um arquivo de uma pasta e colando em outra

Abra a pasta que contém o arquivo que você deseja copiar, clicando com duplo clique sobre a mesma. Estando a pasta aberta, clique uma vez sobre o arquivo que você deseja copiar, em seguida pressione a tecla Ctrl, e sem soltar esta última, clique na tecla C.

Abra então a pasta onde o arquivo copiado será colado. Para colar o arquivo, pressione a tecla Ctrl, mantenha esta tecla pressionada e clique na tecla V.

Se sua foto já estiver na pasta onde será gravada a tua página, então digite sua página conforme o modelo abaixo adaptando as linhas que estão em negrito.

3.3 Os passos para criar um site simples utilizando o programa FrontPage

3.3.1 O planejamento

É imprescindível que você planeje como será o site que você deseja construir. Para lhe ajudar nesta tarefa antes de sentar em frente ao computador seguem algumas perguntas que você precisa responder e planejamentos que você precisa fazer.

a)O que deve constar na primeira página que irá apresentar o teu site (ou o conjunto das tuas páginas) ?

O conteúdo desta primeira página pode ser semelhante a um trabalho escolar com identificação da instituição UNIJUÍ, departamento, curso turma disciplina, título do trabalho autor(aluno), Ijuí, semestre, ano e um link denominado "ENTRAR" que vai para o sumário. O sumário é a segunda página que era aparecer mas uma das ultimas que será concluída. Pois as demais páginas que devem estar prontas para ela poder funcionar.

A diferença principal da primeira página de um trabalho apresentado em forma de páginas, com a capa de um trabalho acadêmico, é a quantia de espaços entre os dados. Tudo deve aparecer numa única tela, sempre que possível, sem precisar utilizar a rolagem de tela. Mas isto também não é proibido.

b) O que deve aparecer no sumário?

Quais são exatamente os termos que serão utilizados neste sumário. Quem entrar no link quer saber antes de entrar se vale à pena ler esta parte ou não.

c)Para cada título e subtítulo do sumário deve ser construída uma página e cada uma destas deve ser planejada. Se estas estiverem prontas no Word, escreva o nome do arquivo de onde deve vir o conteúdo. e onde este se encontra no momento Exemplo: disquete chamado xyz que está guardado em tal local.

d)Se você souber exatamente o que quer que apareça em cada uma das partes da página, então pode passar para o passo seguinte.

Na parte inferior de cada página você precisa colocar pelo menos um link para voltar ao sumário. O melhor é colocar três links denominados de Página Anterior, Sumario e Próxima página.

e)Está tudo decidido? Então já está na hora de ligar seu computador.

3.3.2 Implementação do seu plano

a)Crie uma pasta chamada minha_pagina;

b)Dentro desta você salva todas as telas(páginas independentes que serão chamadas pelos links) e a página principal que será a primeira que abre.

Tudo terá que ser salvo nesta mesma pasta. Nada funcionará se não for colocado tudo ali, sempre.

c)Abra o FrontPage e use-o como se fosse o Word e Digite cada uma das telas ou páginas separadamente. Uma com o objetivo; outra com justificativa, etc.

d)Salve a página que você ainda vai construir antes de iniciá-la com um nome adequado ou seja, nomes pequenos, tudo em minúsculo, sem acento, sem espaços, sem sinais. Pode-se utilizar o sublinhado para dar legibilidade. Exemplos: sumario.htm, objetivos.htm.

e)Digite o título e acione a tecla Enter.

f)Selecione o título que você acabou de digitar e procure Título 1 do menu superior, como se faz no Word. Isto pode estar escondido. procure abrir todas as setinhas até achar Normal com fundo branco e troque isto por Título 1.

g)Digite os subtítulos, se for o caso e marque-os como título 2(ou 3, 4), do mesmo modo como foi feito no Item f.

h)Digite o texto daquela parte específica(só objetivo, ou só tal parte..);

i)Se você já tem tudo digitado no Word, então faça o seguinte para cada uma das partes que irão compor as páginas:

j)Abra o programa Bloco de notas que normalmente se encontra no seguinte local: Iniciar->Programas->Acessórios->Bloco de notas. Ou num outro menu dentro de acessórios.

l)Abra o programa Microsoft Word a partir do arquivo já digitado, clicando sobre o mesmo.

m)Selecione o conteúdo que deve entrar na pagina que você está construindo. No menu do Word, clique em Editar-> Copiar, sem desfazer a seleção. Após a cópia realizada no Word ative o Bloco de notas, clicando sobre este programa, que deve estar aparecendo na barra inferior da tela do computador.

n)Ao abrir o bloco de notas escolha no menu deste bloco, a opção Editar->Copiar. Na verdade você deve copiar do Word e colar no bloco de notas do jeito que você souber fazer.

o)Quando à parte que irá compor uma das páginas estiver toda no programa Bloco de notas, neste mesmo programa clique em Editar->Selecionar tudo.

p)Estando tudo selecionado clique Editar -> Copiar.

q)Tendo a cópia do conteúdo a partir do bloco de notas, ative o programa FrontPage da barra inferior da tela ou abra este programa se foi fechado.

r)Estando com o programa FrontPage ativado, escolha Editar->Colar. Após esta colagem, feche o bloco de notas e o texto do Word.

s)Agora selecione os títulos e subtítulos conforme consta nos itens f e g e reorganize o texto.

Se esta fase de passar o texto todo para o bloco de notas for suprimida, fica muito difícil formatar as páginas caso o conteúdo que será colocado no FrontPage vier de uma cópia direta do Word.

3.4 Inserir figura ou foto na página utilizando o FrontPage

a) Para inserir uma figura, prepare-a no Paint, ou em outro local. Salve ou cole esta ou estas figuras ou fotos dentro da única pasta chamada aqui de "minha_pagina" que você vai usar durante toda confecção e divulgação do trabalho.

b) Para colocar figura, vá em: Inserir ->Figura->Do arquivo e, na janela que abre procure a figura que você quer inserir, clicando nela por aquela janela que se abriu ao clicar em ->Do arquivo antes.

3.5 Inserindo Hiperlink utilizando o FrontPage

Para fazer links com páginas da internet ou com páginas relacionadas entre o site que você está construindo, siga os passos listados a seguir:

a)Se você quiser colocar um link para uma página da internet: Em primeiro lugar você precisa escrever um nome, que você mesmo deve escolher, para o link. Exemplo: "Ver página da Turma de Matemática na modalidade EAD da UNIJUÍ" ;

b)Agora selecione o nome do link que você escreveu, vá em Inserir ->Hiperlink, e na janela que abre, basta você completar o local precedido e URL com endereço completo do site. Exemplo: http://unijui.tche.br/defem/proifen_2006. Em seguida clique em Ok.

c)Se você quiser colocar um link para uma página que está dentro da pasta minha_pagina, é preciso escrever o nome do link, selecionar o nome do link, clicar em Inserir ->Hiperlink, e na janela que abre, basta você completar o local precedido e URL com o nome do arquivo que você deseja abrir pelo link que você está criando. Exemplo: sumario.htm e clicar em Ok.

3.6 Salvando as páginas construídas no FrontPage

a)Salve a página que você acabou de construir na pasta "minha_pagina". Se for o sumário ou a tabela com o que será chamado: salve como sumario.htm, se for introdução salve como introducao.htm, sem acento, sem "ç", sem espaço. Use somente letras, números e ou sublinhado.

Assim tudo que pertencer à sua página(ou seu site), terá que ser salvo somente para aquela pasta "minha_pagina".

3.7 Inserindo Tabelas com o FrontPage

a)Tabelas servem par organizar os dados. Uma tabela poderá ser utilizada para chamar as partes do trabalho através de links. Neste caso terá que ser feito por último.

b)Para inserir uma tabela escolha Tabela->Inserir -> Tabela.

c)Da janela que abre, leia o que se pede e coloque o número de linhas que você precisa, bem como o número de colunas. O restante das informações que aparecem na janela podem ser modificadas. E no final clique em Ok.

3.8 Formatando plano de fundo com o FrontPage

Após a conclusão da digitação do texto, inclusão do links figuras fotos, eliminação de espaços desnecessários, etc. Vá para o menu superior do FrontPage escolha formatar plano de fundo. Leia tudo o que tem de opção. Use pelo menos a opção Plano de fundo e escolha a cor do fundo da página.

Salve a página e verifique se tudo está funcionando conforme esperado.

ATIVIDADES À DISTÂNCIA

Nesta atividade à distância, você deverá fazer o que segue:

a) transformar os trabalhos elaborados em Estatística e em Modelagem para páginas em HTM e acrescentar links na sua página pessoal, construída na primeira etapa do curso, para estas páginas;

b) acrescentar o link da atividade à distância relacionada com situação de estudo, descrita na ATIVIDADE I - Seminários Situação de Estudo.

Obs. Todos estas páginas devem estas dentro de uma mesma pasta. Pasta esta que devera ser nomeada com o teu nome.

Atendimento On-line Programado para Informática no Ensino de Matemática

Endereço para acesso http://www.projetos.unijui.edu.br/matematica/tania

Turma A: Dia 19/04/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia19/04/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 19/04/2006 no turno da noite das 18h:00mim até 22h:00min

Atendimento para Informática no Ensino de Matemática em qualquer horário

Para tirar dúvidas sobre este trabalho, através de mensagens acesse o seguinte endereço: http://www.projetos.unijui.edu.br/matematica/tania clique em deixe seu recado.

O último endereço informado acima funciona 24 horas por dia para recados. Se for colocado o e-mail de quem acessar será dado retorno para este no prazo de 72h.

ATIVIDADE IV

Utilizando a planilha eletrônica na preparação de material didático interativo para o ensino de matemática no Ensino médio

Objetivo:

Analisar material didático elaborado com o Excel.

Aprender a utilizar uma planilha eletrônica para preparar material didático interativo.

Nesta atividade você irá aprender a utilizar o excel como ferramenta para preparação de material didático de matemática para utilização em aulas de laboratório de informática.

4.1 Conhecendo materiais elaborados com o Excel

É importante você conhecer alguns materiais elaborados com o Excel para depois aprender a construir outros desta natureza. Para tal lhe convidamos a entrar no endereço http://www.projetos.unijui.edu.br/matematica/principal/medio/matrizes/index.html ou abrir o CD do curso, e seguir o caminho UNIJUI->Ensino Médio->Matrizes, determinantes e sistemas. Leia o que aparece nas telas, coloque os dados conforme solicitado observe como aparecem as respostas. Prepare uma aula com atividades que você daria para os alunos utilizarem este material. Ele não é auto-suficiente, você precisa preparar material para que o existente tenha sentido.

Passaremos a descrever os passos para elaboração de um material simples utilizando o Excel.

4. 2 Utilização do Excel como calculadora

Utiliza-se + para adição; - para subtração; / para divisão; * para multiplicação; e ^ para potenciação.

A radiciação é transformada para expoente fracionário a fim de utilizar o operador ^. Veja os exemplos que seguem e aproveite para digitar as partes do texto, que aparecem com bordas, no Excel. Cada parte em uma célula específica do excel. Você não deve utilizar a mesma célula para duas instruções distintas.

Para obter o valor de 34 + 20/4 – 3x5 digita-se = 34 + 20/4 –3*5 sempre acionado Enter, após concluir a digitação.

O valor da expressão 2⁸ + é obtido com = 2^8+64^(1/3).

Para obter o valor de digita-se: = ( 2^5 + 3*7 )/( 16^(1/4)-12).

Para digita-se = (( 2^5 + 3*7 )^(1/3) + 65) / (( 6+10)^(1/4)-9).

Obs.: Se faltar algum parêntese, abrirá uma mensagem. Clique em Sim. Depois que a janela fechar, clique duas vezes na célula que foi corrigida automaticamente para ver se o parêntese foi colocado no lugar certo, dentro da expressão. Se clicar em Não você terá que procurar o erro e consertá-lo.Você deve ter percebido que:

a) Para escrever uma expressão que seja calculada no excel, uma fórmula ou instrução, inicia-se o sinal de igualdade ( = ).

b)Os cálculos envolvendo radiciação devem ser escritos na forma de expoente fracionário. Exemplo e no excel digita-se = 32^(1/5).

c)Para fazer agrupamentos, utiliza-se somente parênteses. Não se pode utilizar colchetes e chaves para fazer agrupamentos. Por Exemplo, para obter o resultado de 4-{ 2³-[2 + 4 x 5 + (3-5)³ –5⁴]} no excel digita-se do seguinte modo

= 4- ( 2^3-( 2+4*5+(3-5)^3 – 5^4 ) ).

Exercícios para digitação de expressões numéricas no Excel

Digite as expressões a seguir no Excel conforme exemplos apresentados anteriormente.

Respostas: a)3; b)7; c)3; d)5; e)2; f)81; g)49; h)27; i) 25; j) 32;

k) 2; l)1; m)1,4; n) 772.

4. 3 Indicação de endereços

Uma das características do Excel, mais utilizadas na construção de material didático é a utilização dos endereços onde os valores fornecidos pelos alunos serão colocados.

Figura 1

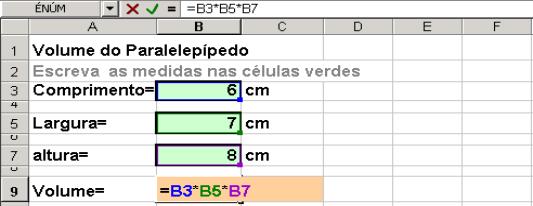
Note que na célula B9, ou seja, na coluna B e linha 9 foi digitado =B3*B5*B7 em vez de digitar 6*7*8, que daria o mesmo resultado do volume, assim que fosse acionado a tecla Enter. A vantagem de escrever o endereço da célula onde está cada um dos valores do cálculo que se deseja efetuar, em vez de colocar os próprios valores, é que se pode muda-los sem alterar a fórmula e o resultado será ajustado automaticamente.

Exercícios

a) Digite tudo o que aparece na figura 1 no Excel.

b) Nesta mesma planilha, substitua os valores do comprimento, largura e altura por 2, 3 e 4 respectivamente e veja se o volume está de acordo com os dados fornecidos por último.

c) Coloque outros valores para comprimento, largura e altura utilizando valores com vírgula(decimais).

d) Elabore uma nova planilha onde se possa obter o valor da área de um retângulo, a partir da medida da base e da altura.

e) Elabore uma nova planilha onde se possa obter o valor da área de um triângulo, a partir da medida da base e da altura.

f) Elabore uma nova planilha onde se possa obter o valor da área de um triângulo, a partir da medida dos três lados.

g) Elabore uma nova planilha onde se possa obter o valor da área de um círculo, a partir da medida do raio.

h) Invente uma atividade para uma das séries em que você atua.

A construção do material que será realizada neste encontro baseia-se na construção de planilhas automatizadas. Para tal, serão descritos os procedimentos mais comuns, na elaboração de planilha para o caso específico de construção de material didático interativo, destinado ao ensino da matemática na Educação Básica.

4.4 Construção de Tabelas de Funções

Os dados do problema a ser resolvido, devem ser digitados, uma única vez, em células destacadas com cor de fundo diferentes e/ou com contorno. No restante da planilha, estes dados devem ser referenciados somente pelo endereço em que cada dado se encontra na planilha. Na figura 2, que mostra a construção de tabela de qualquer função do tipo y=ax+b, o valor do parâmetro a foi digitado na célula C1( coluna C e linha 1) e o parâmetro b foi digitado na célula E1 (coluna E e linha 1)

Figura 2- Construção de uma tabela e gráfico de uma função do tipo y= ax + b

Para utilizar os dados que estão em certa célula em outra célula, ou fazer um cálculo em uma célula, é preciso iniciar a digitação com o sinal de igualdade.

Exemplo: = A4 + 1

4.5 Arrastando Fórmulas

Para arrastar uma fórmula que será adaptada pelo excel para outras células da mesma coluna, mas para linhas diferentes você deve clicar uma vez na célula e, com ajuda do mouse, colocar o cursor na parte inferior direita até aparecer uma cruz preta. Neste momento fique pressionando o botão esquerdo do mouse e vá arrastando a fórmula em questão para as células seguintes.

4.6 Fixando Células

Se, numa fórmula que será arrastada, tiver dados com endereços que serão fixos para todas as linhas, estes endereços deverão ser marcadas com $ antes do número da linha, ou seja, colocar o cifrão entre a letra que indica a coluna e o número que indica a linha da célula que contém o dado fixo. Exemplo = C$1*A4 + E$1. Se a fórmula for arrastada horizontalmente, o cifrão deverá ser colocado antes da letra que indica a coluna fixa.

4.7 Fazendo Gráficos de Funções

Para fazer o gráfico de uma função no excel, em primeiro lugar, é preciso construir uma tabela com cabeçalho. Em segundo lugar deve-se selecionar toda a tabela inclusive o cabeçalho. Em terceiro lugar clica-se no botão da barra superior. Da janela que abre escolhe-se Dispersão(XY) das opções que aparecem no lado esquerdo e a figura de linhas suaves das opções do lado direito. Em seguida clique no botão concluir, que fica na parte inferior da janela. Tendo um pouco de habilidade com o programa excel, pode-se escolher a opção avançar e fazer um gráfico mais qualificado.

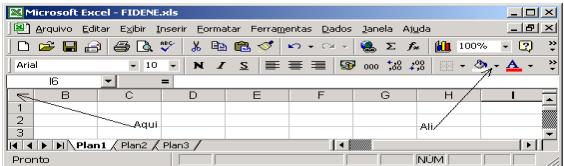
4.8 Colorindo o fundo

Para deixar toda planilha com fundo colorido, sem as delimitações das linhas e colunas que caracterizam o Excel, aciona-se, em primeiro lugar, no botão indicado por uma seta e a palavra “Aqui”, em seguida escolhe-se a cor branca ou outra cor no local indicado pela seta e a palavra “Ali”, conforme mostra a figura 3. Ou selecione uma região que será utilizada para apresentar a atividade e escolha a cor pela opção indicada Poe “Ali”. Esta última forma gera um arquivo mais leve.

Figura 3 - Colocação da cor de fundo em toda planilha

4.9 Colorindo o fundo das células de entrada de dados

Preencha as células onde as os valores de entrada deverão ser digitadas. Na figura 2 os dados de entrada foram colocados nas células C1 e E1 e preenchida com certa cor. Para pintar ou preencher uma célula com certa cor, em primeiro lugar, clica-se na célula que será preenchida, em seguida clica-se no balde de tinta , escolhendo a cor para o fundo pela barra com seta, que fica ao lado do balde.

4.10 Colocando bordas

Colocação de bordas na célula preparada para receber os dados de entrada. Para colocar uma borda numa célula deve-se clicar na célula que receberá a borda e em seguida escolher a borda desejada .

4.11 Alinhamento do conteúdo das células

O alinhamento do conteúdo de cada célula e feito de forma que a estética fique a melhor possível. Para fazer o alinhamento do conteúdo de uma célula, em primeiro lugar, digita-se nesta e em seguida clica-se no botão correspondente que fica na parte superior da planilha. As opções são: para alinhar à esquerda; para centralizar e para alinhar à direita.

4.12 Problemas com textos iniciados com =, +, - , ^ , *

Ao digitar um texto no Excel que inicia com =, +, - , ^ , * pode-se utiliza o apóstrofe para que estes sinais sejam reconhecidos como texto, caso isto não esteja ocorrendo.

4.13 Utilização do comando condicional SE( )Figura 4 - O comando SE( )

Na figura 4, a célula C2 foi programada para escrever a mensagem “Coloque um valor diferente de zero para o coeficiente a”, sempre que o valor digitado para o coeficiente a for igual a zero. Para isto, na célula C2 foi digitado a seguinte instrução:

= SE( C1 = 0 ; "Coloque um valor diferente de zero para valor de a." ; " " ).
Traduzindo esta instrução para linguagem corrente tem-se:

Se o valor que está na célula C1 for igual a zero, então escreva: Coloque um valor diferente de zero para valor de a. Senão coloque só um espaço.

4.14 Utilização do comando condicional OU( )

A utilização do operador lógico OU( ). Na figura 4 aparecem situações em que o aluno terá que colocar as respostas na coluna E. Na coluna F aparecerá a palavra “Certo” se a resposta digitada na coluna E for correta, senão aparecerá a palavra “Errado” na coluna F, da linha correspondente ao exercício.

Figura 5 – A utilização do OU

Tendo duas ou mais condições que dever ser satisfeitas ao mesmo tempo.

Figura 6 - A Utilização do operador lógico E( )

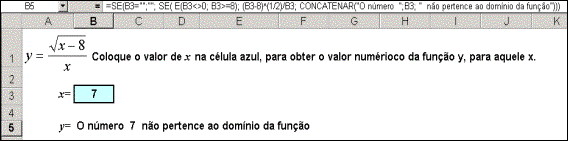
No exemplo mostrado na figura 6, o valor de y que será colocado na célula B5 foi definido foi definida seguinte instrução:

=SE(B3="";""; SE( E(B3<>0; B3>=8); (B3-8)^(1/2)/B3; CONCATENAR("O número ";B3; " não pertence ao domínio da função")))

Traduzindo esta instrução para a linguagem corrente: Se o conteúdo da célula B3 estiver vazia, então deixe o conteúdo da célula B5 vazia, senão( se B3 não estiver vazio), veja se o conteúdo B3 é diferente de zero e, além disto, conteúdo de B3 é maior ou igual a oito, então, neste caso, coloque na célula B5(célula onde a instrução foi escrita) o valor resultante de (B3-8)^(1/2)/B3, senão(se não ocorrer as duas condições B3<>0 e B3>=8) escreva “O número ” ; coloque o valor de B3; e continue escrevendo “ não pertence ao domínio da função".

4.15 Utilização das funções do Excel

Para conhecer todas as potencialidades do Excel para preparação de material interativo para o ensino da matemática, você deve procurar o botão da barra ferramentas que fica na parte superior da planilha. Explore cada uma das funções, lendo para quê serve, e como se usa cada uma das funções. Anote em separado o que lhe interessa.

ATIVIDADE V

Utilizando o Programa MuPAD no Ensino da Matemática

Objetivo:

Conhecer um programa específico com computação numérica, algébrica e gráfica específico para matemática

As atividades a seguir envolvem alguns conteúdos do ensino fundamental e médio. Aproveite para praticar a utilização este aplicativo específico para matemática digitando toda parte do texto que está com borda, o qual é formado por instruções interpretadas pelo programa MuPAD, que você deve instalar em seu computador. O endereço para obtenção deste programa é: http://www.projetos.unijui.edu.br/matematica

Ao digitar as instruções que apare cem na parte do texto com borda alguma delas vem precedida de duas barras //. Tudo o que aparece nas linhas precedidas de // são observações ou comentários que não precisam ser digitado.

5.1 Operações algébricos básicas no MuPAD

O sinal + indica adição. Exemplo 5+1.5 ( acionar enter). O sinal - indica subtração. Exemplo 5-1.5. O sinal ^ indica potenciação. Exemplo 2^3. O sinal * indica multiplicação. Exemplo 3.5*2. O sinal / indica divisão. Exemplo 8/4.

O valor de p é representado por PI. A união dos conjuntos A e B é representado por A union B. A intersecção dos conjuntos A e B é representado por A intersect B e a diferença entre A e B por A minus B

Para restaurar( limpar) a variável x utiliza-se delete x;

Para indicar radicais é utilizado o expoente fracionário. Exemplo 8^(1/3) para expressar

5. 2 Exemplos com os principais recursos do programa

5.2.1 Utilizando recursos da computação numérica

A) Encontre o resultado em forma de fração ordinária , número misto e decimal aproximado:

a)= b) = c) = d)

Para encontrar o resultado da última digita-se

a:=(2/3)/(1/5) ;

Obs.: Após a digitação de cada instrução, colocar-se ; (ponto e vírgula) e aciona-se Enter caso se queira visualizar o resultado. Caso não se queira visualizar o resultado é necessário colocar : ( dois pontos) e acionar Enter.

Para ver a parte inteira, a parte fracionária e o decimal aproximado do último resultado, ao mesmo tempo digita-se:

floor(a), frac(a), float(a) ;

Para traduzir estes comandos para outros “apelidos” que se queira dar aos comandos pode-se digitar o que segue.

alias( parteinteira=floor, partefracionaria=frac, decimal=float );

b:=(2/3)/(1/5);

parteinteira(%) , partefracionaria(%) , decimal(%);

Obs.: O símbolo % pode ser utilizado para substituir a digitação do último resultado obtido.

B)Encontre o resultado de cada uma das expressões:

b) .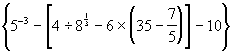

Obs: Utiliza-se somente parênteses para fazer agrupamento no MuPAD. Para obter o resultado da última expressão, digita-se:

( 5^(-3) - ( 4/8^(1/3)-6*( 35- 7/5 ) ) -10);

float( %); // para obter o resultado na forma de decimal

Utilize a calculadora para encontrar o resultado da última expressão da questão 3

5.2.2 Utilizando recursos da computação algébrica

A)Encontre o termo desconhecido:

a) ; b) ; c) ; d) .

A primeira e a última questão estão resolvidas a seguir:

solve( x/69=17/23, x);

alias(resolva=solve); // traduzindo o comando

resolva( (x/4) / 3 = 2 / (3/7), x); // resolvendo última

B)Fatore as expressões

a) ; b) ; d) ; d) ; e) ;

Para encontrar o resultado da fatoração das duas últimas, pode-se digitar:

factor(x^5+1);

alias(fatore=factor);

fatore(x^7+1);

C)Encontre o quociente e o resto da divisões em seguida verifique se existe alguma regularidade nas respostas. É possível fazer alguma régra?

a) b) c) d) e) f)

Para obter os resultados do ítem c e d pode-se digitar:

divide( (x^8+1), (x+1)); // aparecerá o resultado da divisão, seguido do resto

D)Faça o desenvolvimento das potências a seguir e descreva as regularidades que podem ser percebidas:

Para obter o desenvolvimento da última digita-se

expand( (a+b)^3 );

E)Simplifique as expressões

a) ; b) ; c) .

Para simplificar a última digita-se

simplify( x*y*z/(a*z*y) ) ;

normal( x*y*z/(a*z*y) ) ;

F)Resolva as equações algébricas:

a) b) c)

d) e)

Para resolver as últimas digita-se:

solve(x^5-6*x^4-5*x^3+2*x^2-x+7 , x );

float(%);

alias(resolva=solve, decimal=float);

resolva(x^4-5*x^3+2*x^2-x+7 , x );

valores(%);

G) Resolva as diversas equações , inequações e sistemas

a) , b) , c)

d) , e) , f) g);

5. 3 Resolvendo Equações, Inequações e Sistemas

A)Para resolver o sistema do item a) pode-se digitar

s1:={ 6 = x-y , x+y=1 };

solve(s1, [x,y] );

Para resolver as duas últimas pode-se digitar

solve( 2*x-6<8 ,x);

solve( abs(2*x-6) <8 ,x);

5.4 Racionalize os denominadores das seguintes expressões

; ; ; ;

Para racionalizar a primeira e a última expressão digita-se:

5/(3)^(1/2);

4/ 3^(1/3);

5.5 Arredonde os números decimais para números inteiros

a) 20,5 b)20,4 c)20,8 d) 12,2 e)12,5 f) 12,9 g)7,2 i) 7,5 j)7,8

Para arredondar o primeiro valor pode-se digitar o seguinte:

n:=20.5;

trunc(n) ; // despreza todas as casas decimais

floor(n); // arredonda para inteiro igual ou menor que x, mais próximo

round(n) ; // arredonda para inteiro mais próximo

ceil(n); // arredonda para inteiro igual ou maior que x, mais próximo

5. 6 Exemplo de aplicação de resolução de sistemas

Um feirante oferece 3 tipos de sacolas com verduras, todas são vendidas a R$ 2,50. A composição das sacolas é a seguinte:

Sacola tipo 1:

2 maços de cenouras, 3 espigas de milho verde e 1 repolho.

Sacola tipo 2:

3 maços de cenouras, 1 espigas de milho verde e 1 repolho.

Sacola tipo 3:

1 maço de cenouras, 2 espigas de milho verde e 2 repolho.

Deseja-se saber a que preço está sendo comercializado, por este feirante , cada maço de cenoura , cada espiga de milho e cada cabeça de repolho?

>e1:=2*c+3*m+r-2.5;

>e2:=3*c+m+r-2.5;

>e3:=c+2*m+2*r-2.5;

>solve({e1=0,e2=0,e3},[c,m,r]);

>//ou

>sistema:= { 2*c+3*m+r=2.5, 3*c+m+r=2.5, c+2*m+2*r=2.5 } ;

> precouni:=solve(sistema, [c,m,r] );

>// ou somente

>solve( { 2*c+3*m+r=2.5, 3*c+m+r=2.5, c+2*m+2*r=2.5},[c,m,r] );

5.7 Recursos de programação

5.7.1 Procedimentos

Procedimento que pode servir como exemplo para estabelecer relações entre conteúdos

// procedimento para comparar medidas de área e perímetro de retângulos - conteúdo de quinta série

// ATENÇÃO – DIGITAR TODAS O AS LINHAS ABAIXO NUMA ÚNICA LINHA, ACIONAR ENTER SOMENTE APÓS A ÚLTIMA LINHA

retangul:=proc(n)

begin

print( ` base, altura, perímetro, área ` );

for i from 1 to n-1 do

print(i, n-i, 2*i+2*(n-i), i*(n-i) );

end_for;

end_proc;

// executar o procedimento anterior

retangul(10);

5.7. 2 Laços

Segue uma “ malha”, “ laço” ou “loop” para comparar juros simples e juros compostos variando o número de períodos -conteúdo de sexta série.

c:= 100:

i:= 10:

// Obs: digitar as linhas a seguir muna única linha

for t from 1 to 10 do

Js:=float(c*i*t/100) ;

Jc:=float(c*(1+i/100)^t -c);

print( t, Js, Jc)

end_for:

5.8 Operações com Matrizes

Dadas as matrizes

; ;; ; ;

G=[1 3 4 ], efetue as operações a seguir:

a) A+B; b)B+A ; c)A-B; d)B-A; e) AxB; f) BxA; g) D1x E; h)ExD1; i) FxG; j) GxF; k) CxA; l)AxC; m)CxB; n) BxC; o)CxD1; p)Cx F q) 3A; r)A² s) A^-1 ;t) Ax A^-1 ; u)A^-1x A; v)Determinante de A;

Para efetuar as operações dos itens a, f , g, e v digita-se:

// definindo as matrizes A e B de ordem 3 por 3.

A:=matrix( 3, 3, [ [1,2,3] , [5,4,9] , [1,1,6] ] );

B:=matrix( 3, 3, [ [1,3,3] , [2,1,7] , [5,6,9] ] );

A+B; // Efetuando a adição das matrizes-ítem a.
B*A; // Efetuando a multiplicação das matrizes -ítem f.

InvA:= 1/A; //Cálculo da inversa de A -ítem s.

linalg:: det(A); // Calculando o determinante da matriz A-ítem v.

//definindo as matrizes D1_3x2 e E_2x3.

D1:=matrix( 3 ,2, [ [1,2] , [2,0] , [ 1,1] ] ) ;.

E:=matrix( 2 , 3, [ [1,5,1] , [2,3,4] ] ) ;
D1*E; // Ítem g.

5.9 Conjuntos e Intervalos

Dados os conjuntos A = {6, 1, 2, -5, 7}, B = {1, -4, 6, x, 0}, C = {9, -3, 6, x, 1}, faça as operações solicitadas:

a) A È B; b) C Ç A; c) A – B d) AÇC-B; e)A ÇB; f) CÈAÈB;

Para resolver as três primeiras questões acima digita-se:

//Definindo os conjuntos

A:={6, 1, 2, -5,7};

B:={1, -4, 6, x, 0};

C:={9, -3, 6, x, 1};

X:= A union B; // Realizando a união

Y:= C intersect A; // Realizando a intersecção

Z:= A minus B; // Realizando a subtração

Operações com intervalos

Dados os intervalos A= [3, 5] , B=(4, 7), C=[-3, µ), D1=(-µ, 15); E= (3, µ), faça as seguintes operações: a) R – (3, µ); b) AÈB; c)AÇB d)A-B e)D1-A f)D1ÇA g)AÇE

Para definir os intervalos e realizar as três primeiras operações digita-se:

//definindo os intervalos

A:=Dom::Interval( [3, 5] );

B:=Dom::Interval( 4, 7 );

C:=Dom::Interval( [-3],infinity );

D1:=Dom::Interval( -infinity, 15 );

E1:=Dom::Interval(3, infinity);

R:=Dom:: Interval( -infinity, infinity);

R minus A; A union B; A intersect B;

5.10 Definindo fórmulas

A)Dada a fórmula da área do losango A=(Dxd)/2, determinar o valor de A para os seguintes casos:

a) D = 5cm e d=3cm; b) D=10cm e d= 6cm; c) D=15cm e d = 9cm.

Para encontrar o valor de A para o caso c) digita-se:

A:= (D1*d)/2; // Informando a fórmula de A

//c)

D1:=15*cm;

d:=9*cm;

B)Responda com base nos dados que você pode observar no exercício anterior: Se a área de um losango L1 for 20cm². Qual será a área do losango L2 sabendo-se que as medidas das diagonais são o dobro de L1? Justifique.

C)Dada a fórmula: M=C(1+i/100)ⁿ, determinar o valor de M para os seguintes casos:

a) C = 100; i=10; n=2. b) C=200; i= 10; e n=2; c) C=300; i= 10; e n=2.

Para encontrar o valor de M para o caso a) digita-se:

M:=C*(1+i/100)^n; // Informando a fórmula de M

//a)

C:=100;

i:=10;

n:=2;

M; // aparecerá 121

D)Responda com base nos dados que você pode observar no exercício anterior: se o valor de C fosse 1000, e os demais valores continuassem os mesmos que no exercício anterior, você poderia dizer qual seria o valor do montante, sem refazer todos os cálculos?

5. 11 Dada uma fórmula, isolar alguma das variáveis envolvidas

A) Dada a fórmula do comprimento da circunferência C=2 p r, isolar a variável r.

Para isolar r da fórmula acima digita-se:

delete C; // restaurando a variável C que foi utilizado na atividade anterior.

r = solve(C = 2*PI*r, r); // Dentro do solve( ), utiliza-se somente “=”, sem dois pontos.

B)A fórmula do valor à vista Va de uma mercadoria que será parcelada em n parcelas mensais e iguais a P a uma taxa unitária mensal fixa de i é dada por Va=P[1-(1+i)^-n]/i.

Isole P da fórmula acima para o caso em que i = 0,04 , n valendo de 1 até 10, utilizando um valor de n cada vez.

Para isolar P da fórmula acima e conhecendo-se i=0,04; n = 1 e n = 2 digita-se:

i:=0.04; n:=1;

P = solve(Va = P*(1-(1+i)^(-n) )/i , P);

n:=2;

P = solve(Va = P*(1-(1+i)^(-n) )/i , P);

n:=3;

P = solve(Va = P*(1-(1+i)^(-n) )/i , P);

// O restante é com você. Analise as respostas e descubra para que serviriam as respostas. Discuta com seus colegas ao lado. Mais tarde discutiremos em grande grupo.

C) Invente uma atividade similar à 1º ou 2º , com uma fórmula que você conhece e utiliza com seus alunos, e envie uma mensagem para a professora.

5.12 Resolvendo questões passo a passo

A)Dadas as equações de segundo grau a baixo, encontre a solução utilizando a fórmula de Báskara e mostrando os passos utilizados na sala de aula:

a) x²+ 2x + 1=0; b) x²-5x + 6=0; c) x²+ 5x + 6=0; d) x²+ 5x + 4 = 0; e) x²+ 4x +4=0;

Para resolver a primeira equação pode-se digitar:

Delta:=b^2-4*a*c;

x1:=( -b+(Delta)^(1/2) )/(2*a) ;

x2:=( -b-(Delta)^(1/2))/(2*a);

a:=1; b:=2; c:=1; // para as demais reescrever somente as linhas a partir daqui;

Delta;

x1; x2;

Entre outras alternativa pode-se resolver a primeira equação digitando:

a:=1; b:=2; c:=1;

x1:=( -b + (b^2-4*a*c)^(1/2) )/(2*a);

x2:=( -b - (b^2-4*a*c)^(1/2) )/(2*a);

//para as demais equações, refazer tudo para cada equação ou copiar, colar e arrumar

B)Dados dois pontos A e B do plano cartesiano, encontrar uma equação da reta que passa por estes pontos, para dada caso:

a) A(0, 5) e B(2, 6) ; b)A(3, 4) e B( 0, 5); c) A( 0, 6); B(1, 12);

Para fazer a primeira pode-se digitar:

M:=matrix( 3,3, [ [x, y , 1], [0, 5, 1], [2, 6, 1] ] ) ;

linalg::det(M)=0;

x1:=0; y1:=5; x2:=2; y2:=6;

sistema:={ y1 = a*x1 + b, y2 = a*x2 + b};

c:=solve(sistema, [a , b] );

a:=0.5; b:=5;

y=a*x +b;

delete a, b; //Para limpar as variáveis a e b que serão utilizadas como incógnitas no //próximo exercício.

Obs: Os comando a seguir só funcionarão se ao instalar ou abrir o programa foram colocados os números do registro gratuito.

5.13 Gráficos de funções

Para obter num só plano os gráficos das seguintes funções y= x+3, y=x-2, y=x+7 e y =2x² – 4x + 2 digita-se:

plotfunc2d( x+3, x-2, x+7, 2*x^2 –4*x + 2 );

5.14 Gráficos de relações representadas na forma implícita

plot(plot::implicit((x-2)^2+(y-3)^2 = 16,x=-10.10, y= -10.10));

Bibliografia

D’EÇA, Teresa Almeida.NetAprendizagem-A Internet na Educação. Editora Porto, 1998.

LOLLINI, Paolo. Didática e computador: quando e como a informática na escola. Loyola, 1991. 240 p.

ROCHA, Ana Regina, CAMPOS, Gilda H. Avaliação da qualidade de software educacional. Em Aberto, Brasília, v.12, n.57, p.32-43, jan/mar, 1993.

STILBORNE, Ann e Heidi Linda. Guia do Professor para a Internet. Porto Alegre, Editora Artes Médicas Sul, 2000, tradução Edson Furmankiewz.

VALENTE, Armando José. Computadores e conhecimento: repensando a educação. Campinas, UNICAMP, 1993.

Site

http://www.projetos.unijui.edu.br/matematica/ Acesso em 01 mar. 2006.

http://www.projetos.unijui.edu.br/matematica/ccpmem Acesso em 01 mar. 2006.

http://www.mupad.de Acesso em 01 mar. 2006.

MODELAGEM MATEMÁTICA

Prof.ª Denise Knorst da Silva[5]

Endereços: R. Reinoldo Stenhaus, n.º 65, Bairro Morada do Sol, Ijuí – 98700 000

E-mail denisek@unijui.tche.br

Fones: 55 3332 0269- Profissional 55 3331 2142 –Residencial

Página http://www.projetos.unijui.edu.br/matematica/denise

Na Formação Continuada de Professores de matemática do Ensino Médio é de fundamental importância considerar as atuais propostas curriculares para este nível de ensino. A Modelagem e as Investigações Matemáticas serão abordadas como alternativas quando pretende-se promover um ensino que atenda as recomendações dos PCNEM (1999), que contemplam o desenvolvimento de habilidades e competências pelos jovens, resumidas em três grandes eixos: representação e comunicação, investigação e compreensão, contextualização sócio-cultural.

Tomando como base o conhecimento da realidade do educando e da comunidade na qual se insere, a Modelagem Matemática será apresentada e discutida como forma de promover a interdisciplinaridade, a contextualização de conteúdos de matemática, o espírito de investigação e a problematização de situações reais.

A possibilidade das Investigações nas aulas de matemática será discutida a partir do seu significado enquanto processo organizado que envolve conceitos, procedimentos e representações matemáticas e fortemente caracterizado por seu estilo de conjectura-teste-demonstração.

As atividades objetivam promover discussões em torno dos processos que conduzem ao trabalho com Modelagem e Investigações Matemáticas, apresentando-se situações práticas, para que haja reflexão em torno das implicações e potencialidades destas no ensino da matemática. Além disso, atividades de orientação foram acrescentadas no material, entendendo-se imprescindível que o professor seja incentivado, acompanhado e orientado na elaboração de situações capazes de permitir a implementação gradativa das tendências discutidas, na sua prática de sala de aula.

ATIVIDADE I

Explorando Temáticas

Objetivos:

-Reconhecer em diferentes temas a potencialidade para a contextualização de conteúdos de matemática do Ensino Médio;

-Valorizar a transversalidade nos temas abordados;

-Desencadear discussões em torno da importância e das possibilidades de abordar aspectos relacionados ao desenvolvimento da cidadania nas aulas de matemática;

-Socializar as produções e reflexões no coletivo da disciplina.

Descrição:

1-Distribuição, em pequenos grupos, de cartazes contendo figuras e artigos relacionados aos seguintes temas:

Profissões

Transportes

Construção Civil

Alimentação

Orçamento Familiar

Localização

Esportes

Tempo

2-Analisar a importância da temática destinada ao grupo quando trabalhada como desencadeadora de situações didático-pedagógicas para o Ensino Médio, destacando-a como justificativa de seu uso.

3-Listar possíveis atividades, conceitos matemáticos e discussões acerca da temática destinada ao grupo.

4-Realização de debate coletivo sobre as possibilidades discutidas nos pequenos grupos.

ATIVIDADE II

Modelagem Matemática

Objetivos:

- Discutir as possibilidades da Modelagem Matemática enquanto estratégia de ensino e aprendizagem de matemática;

- Discutir a implementação da Modelagem Matemática no Ensino Médio, implicações e os argumentos para esta.

Descrição:

1-Abordagem da Modelagem Matemática: Matemática Aplicada e Educação Matemática.

2-Realizar leitura do artigo: Modelagem Matemática: O que é? Por que? Como?[6].

3-Discussão do artigo nos grupos, tendo por referência questões como:

- O entendimento que o grupo possui de Modelagem Matemática;

- Viabilidade da Modelagem Matemática e implicações para o Ensino Médio;

- Considerações sobre a classificação proposta para as experiências de Modelagem (caso 1, caso 2, caso 3).

4- Desenvolver o problema proposto no artigo para o Caso 1 - decidir pelo melhor plano de pagamento disponível no mercado para ter acesso a internet, tendo presente a coleta de preços apresentada:

	Assinatura Mensal (R$)	Tempo de acesso incluído (h)	Tempo adicional por hora (R$)
Plano 1	17,95	-	0,73
Plano 2	27,95	15	0,53
Plano 3	49,95	60	0,35
Plano 4	75,95	150	0,35

5-Discussão coletiva do artigo, apresentando as considerações feitas pelos grupos.

6-Exploração de processos de Modelagem Matemática produzidos em componentes curriculares do Curso de Matemática-Licenciatura da UNIJUÍ, para seu aproveitamento no Ensino Médio.

ATIVIDADE III

Uma Situação de Modelagem

Objetivos:

-Analisar uma experiência de modelagem;

-Apresentar formas de implementação da modelagem;

-Reconhecer a viabilidade da modelagem para a Educação Básica.

Descrição:

1-Apresentar a situação abaixo ilustrativa da implementação da modelagem:

TEMA: Gás Natural Veicular (GNV)

JUSTIFICATIVA[7]:

Em meados dos anos 80, se dá início no Brasil a corrida para o desenvolvimento de novas fontes energéticas alternativas, com o objetivo primeiro de substituição do óleo diesel. Nessa época, o diesel correspondia a mais de 50% do consumo energético em todo o País, enquanto que o Gás Natural pouco menos de 2% desse total. A partir daí começam a surgir os primeiros planos experimentais, assim como os primeiros programas brasileiros de incentivo à nova fonte energética (GNV).

O uso do GNV é incentivado pelo governo e de interesse dos consumidores em função das boas qualidades intrínsecas que o compõem, do ponto de vista da preservação ecológica e do seu preço atrativo, caracterizando o Gás Natural como sendo a melhor alternativa de combustível no Brasil e no mundo. O ritmo de crescimento da mais nova fonte alternativa de combustível, se dá pelo interesse das companhias distribuidoras, de investirem pesado nos projetos de ampliação de novos postos de abastecimento por todo o país.

O GNV, representa uma importante alternativa, já que entre todos os outros combustíveis utilizados é o que menos agride o meio ambiente e apresenta o menor custo.

O uso de GNV reduz a emissão de poluentes no ar, contribuindo para a melhoria da qualidade de vida. É reconhecidamente mais seguro do que os outros combustíveis. É mais leve que o ar e, em caso de vazamentos, se dissipa rapidamente na atmosfera. Além disso, é um bom aliado para o bolso do consumidor, que economizará até 70% em gastos com o veículo.

O GNV, então, ao ser estudado nos permitirá obter maiores informações sobre este combustível, minimizando dúvidas e viabilizando opiniões e atuações enquanto consumidores conscientes.

Potanto um processo de Modelagem é coerente com a proposta dos PCNME (1999):

A matemática no Ensino Médio tem um valor formativo, que ajuda a estruturar o pensamento e o raciocínio dedutivo, porém também desempenha um papel instrumental, pois é uma ferramenta que serve para a vida cotidiana e para muitas tarefas específicas em quase todas as atividades humanas.

No ensino da matemática, então, faz-se necessária a abordagem de situações que permitam formar no aluno a capacidade de resolver problemas reais, a fim gerar hábitos de investigação, proporcionar confiança e desprendimento para analisar situações novas, propiciando uma visão ampla e científica da realidade.

INVESTIGAÇÃO[8]

Segundo Almeida (2004) a idéia de analisar este problema surgiu a partir de uma reportagem da revista Veja que abordava este assunto e tratava da importância em usar o gás natural como combustível automotivo especialmente no que diz respeito à conservação do meio ambiente.

O início do trabalho deu-se com uma análise das viabilidades, vantagens e desvantagens de um carro cujo combustível é a gasolina em relação a outro que consome gás natural. Foi possível verificar junto a profissionais da área que o processo de conversão é bastante simples, mas que, no entanto, tem um custo médio de R$ 3.000, 00 nas oficinas especializadas da região.

O preço do litro da gasolina e do metro cúbico de gás natural bem como o consumo médio de um carro popular com cada um destes combustíveis é apresentado no Quadro 1 a seguir.

Quadro 1 – preço dos combustíveis e consumo

	Gasolina	Gás natural
Preço	R$ 2, 06 (litro)	R$ 0, 939 (m3)
Consumo	12 Km/L	15 KmL

Obs: Preço dos combustíveis em 12/03 em Londrina

Optando-se por implementar a modelagem através do caso 1^[9], o professor fornece as informações acima e propõe:

Há compensações na conversão de um veículo a gasolina para o GNV? Qual é a relação custo-benefício?

A partir destas informações desencadeia-se o processo de investigação do problema pelos alunos, cabendo ao professor orientar o processo e valorizar as estratégias de cada grupo de trabalho no coletivo da turma.

Os alunos poderão obter um modelo matemático que descreve o gasto com combustível para automóveis que funcionam com cada um dos referidos combustíveis, caso não o obtenham cabe ao professor mostrar essa estratégia de resolução do problema, destacando que:

- as expressões apresentadas no Quadro 2, onde x representa a quilometragem dos automóveis; C1(x) e C2(x) representam os gastos com gasolina e com gás natural respectivamente.

Quadro 2 – custo total em função dos quilômetros rodados

	Carro a gasolina	Carro a gás natural
Custo	C1(x) = 0,17 x	C2(x) = 0,0626 x + 3.000

1. Por meio do gráfico abaixo ou a partir da construção de uma tabela envolvendo as duas funções e várias quilometragens, é possível comparar os valores gastos com cada um dos combustíveis e analisar a viabilidade de cada um.

Figura 1- Gráfico das funções lineares

A interpretação dos dados por meio da análise do gráfico permite concluir, em relação aos gastos, que o carro à gasolina é mais vantajoso para percursos de até 28.000 Km. Por outro lado, se o usuário do veículo percorrer longos trajetos, o seu gasto será bem menor se o carro for abastecido com gás natural, mesmo considerando o valor despendido com a transformação do carro.

As considerações acima permitem afirmar que atingidos 28000 km obtém-se benefício, permitindo pagar o investimento da conversão e perceber a diferença entre o custo da Gasolina e do GNV.

Uma nova questão pode ser abordada: Qual é o tempo necessário para o retorno financeiro do investimento?

Facilmente poderá ser verificado que o tempo para se atingir os 28000Km depende da quilometragem média feita pelo usuário em questão, ou seja:

T (d) = 28000/d onde: T é o tempo em dias

d é a média diária de Km rodados

Assim, é possível estimar, mediante a utilização do modelo, o tempo necessário para que um usuário obtenha retorno financeiro ao converter seu carro a gasolina para GNV.

Texto de Jonei Cerqueira Barbosa [doc] [PDF]

Algumas Considerações

Analisando a situação e seu possível desenvolvimento em uma turma de Ensino Médio, percebe-se a viabilidade da modelagem como um processo gradativo, em que o aluno é convidado para um ambiente de aprendizagem em que a problematização e a investigação são os princípios. O desenvolvimento de habilidades e competências, propostas pelos PCNEM, são possíveis pelo trabalho destacando-se todos os eixos: representação e comunicação, investigação e compreensão, contextualização sócio-cultural.

Os conceitos matemáticos podem ser construídos a partir da modelagem, cabendo ao professor formalizá-los ou introduzi-los durante ou após o processo.

Podemos perceber que a estatística e a informática podem aparecer em diferentes momentos de um ambiente de modelagem: inicialmente, quando busca-se conhecer o tema com maior profundidade, no tratamento das informações coletadas, na problematização, na investigação, na análise dos resultados, enfim, são recursos que permitem a compreensão da situação real e a sua investigação. A empregabilidade destes recursos não é gratuita, deve-se ao fato de estarmos inseridos, sócio-culturalmente, em contextos cada vez mais regidos pelas tecnologias da comunicação e informação.

ATIVIDADE IV

Embalagem – Construção e Modelagem

Objetivos:

-Aprofundar conhecimentos sobre Modelagem Matemática;

-Explorar conceitos geométricos do Ensino Médio;

-Reelaborar concepção e forma de abordagem da geometria bi e tridimensional;

-Valorizar a contextualização no ensino da matemática, de forma a trabalhar sua dimensão social e crítica;

-Desenvolver a Modelagem Matemática.

Descrição:

Entendendo-se que, a partir da criação de uma embalagem, diferentes conteúdos matemáticos de geometria poderão ser abordados, propõe-se que:

Parte I – Exploração da embalagem e do produto

1. Pense num produto a ser embalado (algo já existente, um produto caseiro, algo engraçado, algo muito necessário, algo revolucionário,..);

Obs.: Coloque-se no papel de aluno de Ensino Médio, para imaginar que produto gostaria de colocar em uma embalagem, criado por ele ou já existente.

2. Caracterize o produto (receita, fabricação, cuidados, utilidade,..);

3. Crie uma embalagem para este produto, justificando a escolha e caracterizando sua construção, destacando e explorando conteúdos matemáticos utilizados;

4. Coloque na embalagem todas as informações necessárias ao consumidor e exigidas pelos órgãos responsáveis pelo controle do produto;

5. Priorize na embalagem idéias de estética e marketing;

6. Determine o preço do produto, fazendo os cálculos quanto ao custo, margem de lucro, transporte, estimativa de venda,..

Parte II – Modelagem Matemática

A Modelagem Matemática pode acontecer a partir da construção da embalagem, desta forma, propõe-se:

Defina um problema, relacionado à construção da embalagem ou ao produto em questão, e desenvolva o processo de Modelagem Matemática.

ATIVIDADE V – À DISTÂNCIA

Implementação da Modelagem Matemática

Objetivos:

-Interagir com o coletivo escolar, reconhecendo nos elementos seus papéis na constituição da complexidade do espaço e ato educacional;

-Reconhecer o papel do docente pesquisador na preparação de aulas de matemática;

-Reelaborar concepções acerca do processo de ensino e aprendizagem de matemática;

-Investigar as possibilidades de implementação da Modelagem Matemática na Educação Básica.

Descrição:

A partir de discussões e atividades realizadas no Curso, sobre as possibilidades de implementação da Modelagem Matemática na Educação Básica, organizar e desenvolver uma proposta de implementação da mesma junto ao Ensino Médio. Para tal:

-é necessário definir uma turma de Ensino Médio;

-organizar a implementação mediante:

Escolha de um tema;

Justificativa do tema;

Pesquisa de Campo, coleta de dados, pesquisa bibliográfica,..

Problematização;

Investigação;

Resolução;

Discussão dos resultados.

-desenvolvimento do trabalho, sendo relevante a atenção sobre a participação dos alunos em todo processo, na condução da atividade como um todo, nas dificuldades, nas intervenções solicitadas ao professor,.., para fins de registro e reflexão. (Caso seja possível filmar ou gravar a aula, torna-se interessante).

- Estruturação de um texto descritivo e reflexivo sobre o desenvolvimento da atividade, podendo conter fragmentos de falas interessantes e relevantes dos alunos e professores.

Apresentação da atividade no Seminário da etapa 2 – presencial na forma oral e entrega em disquete ou CD.

Atendimento On-line Programado para Modelagem

Endereço para acesso: http://www.projetos.unijui.edu.br/matematica/denise

Turma A: Dia 11/04/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia 11/04/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 11/04/2006 no turno da noite das 18h:00mim até 22h:00min

Atendimento em Modelagem por mensagens em qualquer horário

Para tirar dúvidas sobre este trabalho,através de mensagens acesse o seguinte endereço: http://www.projetos.unijui.edu.br/matematica/denise e clique em deixe seu recado.

O último endereço informado acima funciona 24 horas por dia para recados. Se for colocado o E-mail de quem acessar será dado retorno para o E-mail informado pelo aluno dentro de 72h.

ATIVIDADE VI

Investigações Geométricas

Objetivos:

-Reconhecer as investigações em sala de aula como mais uma alternativa metodológica para o Ensino Médio;

-Explorar conceitos matemáticos do Ensino Médio utilizando investigações;

-Estabelecer conexões entre os conceitos matemáticos.

Descrição:

-Apresentação de lâmina sobre os passos do processo de investigação para a sala de aula[10].

Investigações Matemáticas - Uma Possibilidade Metodológica

O princípio da pesquisa permeando as diferentes atividades humanas é o ápice do progresso de um povo; não o é diferente em se tratando da educação, e em particular, da matemática. Pesquisar assemelha-se com investigar, inquirir, procurar conhecer o que não se sabe.

Se analisarmos o processo de criação da Matemática, talvez nos deparemos com processos de investigação do homem ao longo da História e, portanto, possamos encará-la como

[..] um organismo vivo, impregnado de condição humana, com as suas forças e as suas fraquezas e subordinado às grandes necessidades do homem na sua luta pelo entendimento e pela libertação; aparece-nos, enfim, como um grande capítulo da vida humana social.(CARAÇA apud PONTE, 2003, p. 16)

A visão da matemática como processo de/em construção talvez possa ser evidenciada mediante atividades de investigação e com estas, enquanto educadores, seja possível desencadear aprendizagens matemáticas significativas.

Aprender Matemática não é simplesmente compreender a Matemática já feita, mas ser capaz de fazer investigação de natureza matemática (ao nível adequado a cada grau de ensino). Só assim se pode verdadeiramente perceber o que é a Matemática e a sua utilidade na compreensão do mundo e na intervenção sobre o mundo. Só assim se pode realmente dominar os conhecimentos adquiridos. Só assim se pode ser inundado pela paixão “detetivesca” indispensável à verdadeira fruição da Matemática. Aprender Matemática sem forte intervenção da sua faceta investigativa é como tentar aprender a andar de bicicleta vendo os outros andar e recebendo informação sobre como conseguem. Isso não chega. Para verdadeiramente aprender é preciso montar a bicicleta e andar, fazendo erros e aprendendo com eles. (BRAUMANN apud PONTE, 2003, p.19)

Algumas Questões Iniciais Sobre Investigações

Pode o trabalho de investigação dos matemáticos servir de inspiração para o trabalho a realizar por professores e alunos nas aulas de matemática?

Qual o papel das investigações no processo de ensinar e aprender matemática?

O que significa investigar?

O que Significa Investigar?

Investigar significa que formulamos questões que nos interessam, para as quais não temos resposta pronta, e procuramos essa resposta de modo tanto quanto possível fundamentado e rigoroso.

Investigar não representa obrigatoriamente trabalhar em problemas muito difíceis, mas que se apresentam no início de modo confuso, mas que procuramos clarificar e estudar de modo organizado.

As investigações matemáticas envolvem, naturalmente, conceitos, procedimentos e representações matemáticas, mas o que mais fortemente as caracteriza é este estilo de conjectura-teste-demonstração.

Investigar em Matemática

..é descobrir relações entre objetos matemáticos conhecidos ou desconhecidos, procurando identificar as respectivas propriedades.

Momentos na Realização de uma Investigação

Exploração e formulação de questões	Reconhecer uma situação problemática Explorar a situação problemática Formular questões
Conjectura	Organizar dados Formular conjecturas e fazer afirmações sobre uma conjectura
Testes e reformulação	Realizar testes Refinar uma conjectura
Justificação e avaliação	Justificar uma conjectura Avaliar o raciocínio ou o resultado do raciocínio

As Investigações como Tarefas Matemáticas

As investigações matemáticas constituem uma das atividades que os alunos podem realizar e que se relacionam, de muito perto, com a resolução de problemas.

Problema: é uma questão para a qual o aluno não dispõe de um método que permita a sua resolução imediata;

Exercício: é uma questão que pode ser resolvida usando um método já conhecido;

Os exercícios e problemas têm em comum a característica de o enunciado indicar claramente o que é dado e o que é pedido. Não há margem para ambigüidades. A solução é sabida de antemão, pelo professor, e a resposta do aluno ou está certa ou está errada.

Numa INVESTIGAÇÃO, trata-se de situações mais abertas – a questão não está bem definida no início, cabendo a quem investiga um papel fundamental na sua definição. E uma vez que os pontos de partida podem não ser exatamente os mesmos, os pontos de chegada podem ser também diferentes.

Condição Fundamental da Aprendizagem

O envolvimento ativo do aluno, mobilizando os seus recursos cognitivos e afetivos na formulação de questões a estudar. O aluno é chamado a agir como um matemático, não só na formulação de questões e conjecturas e na realização de provas e refutações, mas também na apresentação de resultados e na discussão e argumentação com os seus colegas e o professor.

Implicações do uso de Investigações

Ruptura no contrato didático;

Postura docente adequada;

Tempo pedagógico;

Papel ativo do aluno;

Desenvolvimento de habilidades de análise e argumentação;

Ruptura na hierarquia e linearidade dos conteúdos;

Com a turma organizada em grupos, desenvolver atividades de investigação, a seguir:

Algumas Possibilidades de Investigações Geométricas

NVESTIGAÇÃO 1 - A mesa de snooker

Imagine que a figura abaixo represente uma mesa de snooker. Jogando-se a bola de um dos cantos, sem efeito e numa direção que faz um ângulo de 45º com as tabelas (cantos onde a bola bate, considerando também a caçapa, mas não o ponto de partida), suponha que a bola só pare antes de ser encaçapada, na mesa de 6x4:

Por quantos quadrados a bola vai passar? e para mesas de outras dimensões:

1. Como podemos determinar o número de quadrados pelos quais a bola passa?

2. Qual o número de tabelas?

INVESTIGAÇÃO 2 - Quadrados em quadrados

Num quadrado podem-se inscrever outros quadrados. De entre eles, considere aqueles cujos vértices são os pontos de intersecção das quadrículas com os lados do quadrado inicial.

Num quadrado como este, quantos quadrados nestas condições poderá inscrever?

Desenhando quadrados alargue seu estudo a quadrados com dimensões diferentes, investigando possíveis relações entre o quadrados inscritos e o quadrado inicial.

INVESTIGAÇÃO 3 – Teorema de Pitágoras

“Num triângulo retângulo o quadrado da hipotenusa é igual a soma dos quadrados dos catetos”.

Se construir outras figuras geométricas, em vez de quadrados, a relação entre as áreas mantém-se? (demonstre).

INVESTIGAÇÃO 4 - O quadrado e o octógono regular

Um marceneiro quer transformar uma mesa de forma quadrada em outra com oito lados iguais.

Investigue: Como deve proceder o marceneiro?

Conexões Numéricas e Geométricas

INVESTIGAÇÃO 5 - Analise a seqüência de quadrados perfeitos:

CONCLUI-SE QUE:

Para obter um quadrado de lado n + 1 é necessário adicionar o número ímpar 2n +1 ao quadrado de lado n.

Assim, dá-se sentido geométrico à relação (n + 1)²= n²+ 2n + 1.

OUTRA EXPLORAÇÃO POSSÍVEL:

Qual a relação existente entre a representação geométrica acima e os números 1, 3, 5, 7,…

Realizar sistematização das investigações realizadas, no grande grupo, discutindo hipóteses, estratégias, resultados e justificações.

Registrar o trabalho realizado de forma a refletir sobre o mesmo e aproveitá-lo como exploração de conceitos geométricos do Ensino Médio.

Buscar em livros didáticos ou outras fontes uma situação que possa ser trabalhada através da investigação, destacando o conteúdo e sua possível exploração.

Referências

ALMEIDA, L. M. W.. Modelagem Matemática e Formação de Professores. In: V

ANPEd- SUL, 2004, Curitiba. Anais do V Seminário de Pesquisa em Educação da Região Sul. Curitiba: Universidade Católica do Paraná, 2004.

BARBOSA, J.C. Modelagem Matemática em Cursos para Não-Matemáticos. In: CURY, H. N. Disciplinas matemáticas em Cursos Superiores: reflexões, relatos, propostas. Porto Alegre: EDIPUCRS, 2004.

BARBOSA, J.C. Modelagem Matemática: O que é? Por que? Como? Veritati, n.4, p. 73-80. 2004.

BRASIL. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais: Ensino Médio: Ciências da Natureza, Matemática e suas Tecnologias. Brasília: Ministério da Educação/Secretaria de Educação Média e Tecnológica, 1999.

HISTÓRIA DO GNV. Disponível em: <http://www.brunoautoeletrico.com.br/gnv.htm> Acesso em: 04 de jan. 2006.

PONTE, J. P.; BROCARDO, J; OLIVEIRA, H. Investigações Matemáticas na Sala de Aula. Belo Horizonte: Autêntica, 2003.

Site

http://joneicb.sites.uol.com.br/publi.html Acesso em 10 de jan 2006.

http://www.projetos.unijui.edu.br/matematica/modelagem

ESTATÍSTICA

Rosane Maria Kirchner [11]

Endereços DEFEM/ Rua São Francisco 501 B. São Geraldo, Ijuí – 98700 000

Fone: 55 3332 0229 –Profissional 55 3332 4894 -Residencial

E-mail: rosanek@unijui.tche.br

Página: http://www.projetos.unijui.edu.br/matematica/rosane

Neste tópico é abordado o estudo de parte da Estatística, ciência presente em todas as áreas, visando a obtenção de informações a partir de dados numéricos e/ou categóricos. Ela integra um conjunto de metodologias, incluindo desde o planejamento, coleta, tabulação, organização, análise e interpretação de dados. A mesma se constitui em ferramenta eficiente e eficaz, favorecendo e influenciando no processo decisório.

Os temas serão desenvolvidos em três etapas, incluindo teoria e prática, proporcionando ao docente embasamento, acompanhamento e leitura de fenômenos físicos e sociais, fornecendo subsídios à promoção da interdisciplinaridade e da contextualização do ensino com base no conhecimento do contexto vivenciado pelo estudante.

A primeira etapa consiste em um referencial conceitual envolvendo técnicas de estatística descritiva e sua aplicabilidade, possibilitando o desenvolvimento de metodologias para a construção de instrumentos de pesquisa de campo que respondam a indagações referentes às situações de estudo que emergirem. Complementando e favorecendo a operacionalização da teoria, será utilizado o software Excel.

A segunda etapa compreende a estruturação de um instrumento de pesquisa, sendo que o mesmo será aplicado nas instituições de ensino onde os docentes atuam, posteriormente, serem codificados.

Na terceira etapa, os resultados serão sistematizados, viabilizando, dependendo do interesse e do teor das informações obtidas, bem como a profundidade da análise realizada, publicação em forma de artigos científicos em periódicos da área e apresentados em eventos científicos.

ATIVIDADE I

Conceitos básicos de Estatística

Objetivo:

-Informar e compreender conceitos elementares em Estatística.

A parte da estatística que se preocupa apenas em descrever e analisar um dado grupo, sem tirar conclusões ou inferências sobre um grupo mais vasto, é designada Estatística Descritiva ou Dedutiva.

Se uma amostra é representativa da população, pode-se, muitas vezes, tirar conclusões importantes sobre a população inferidas da análise da amostra. A parte da estatística que analisa as condições sob as quais tais inferências são válidas é designada por Estatística Inferencial ou Inferência Estatística.

1.1 Conceitos básicos

População – É um conjunto completo de todos os elementos (pessoas, coisas, objetos, etc.) que tem pelo menos, uma característica comum a ser estudada. Pode ser finita ou infinita. Exemplo: População; Alunos de uma determinada cidade. Variáveis; idade, gênero, procedência.

Censo – Um censo é um conjunto de dados relativos a todos os elementos de uma população.

Amostragem – É o processo de coleta das informações de parte da população (amostra), mediante métodos adequados de seleção destas unidades.

Amostra- É qualquer subconjunto finito (ou parte) de elementos extraídos de uma população. Duas considerações devem ser feitas sobre o estudo amostral dos fenômenos:

a)Deve-se tomar cuidado para que a amostra seja representativa de toda a população;

b)Precisão dos dados coletados, buscando minimizar os erros.

Parâmetro – é uma medida numérica que descreve uma característica estabelecida para toda uma população. Representado por letras gregas. Ex: m (média populacional), s² (variância populacional), s (desvio padrão populacional).

Estimador - é uma medida numérica que descreve uma característica estabelecida para uma amostra. Representada por letras do alfabeto latino. Ex: (média amostral), S² (variância amostral), S (desvio padrão amostral).

1.2 Variáveis estatísticas

A cada fenômeno corresponde um número de resultados possíveis. Assim, por exemplo:

Para cada fenômeno “número de estudantes das escolas de ensino médio do RS” há um número de resultados possíveis expressos através dos números naturais;

Para o fenômeno “peso dos estudantes das escolas ensino médio RS” temos uma situação diferente, pois os resultados podem tomar um número infinito de valores numéricos dentro de um determinado intervalo;

Para o fenômeno “cor dos olhos”, os resultados possíveis são: azul, verde, castanho e preto.

Portanto, variável é, convencionalmente, o conjunto de resultados possíveis de um fenômeno.

Os exemplos que acabamos de ver, nos dizem que, conforme suas características particulares, as variáveis, podem ser classificadas da seguinte forma:

a) Quantitativas: são aquelas que podem ser expressas em termos numéricos. Em geral, são resultantes de medições, enumerações ou contagens. São subdivididas em contínuas e discretas, conforme abaixo:

Contínuas: são aquelas que podem assumir qualquer valor num certo intervalo de medida, podendo ser associadas ao conjunto dos números reais. Exemplo: medidas de tempo, comprimento, espessura, área, volume, peso e velocidade.

Discretas: são aquelas que só podem assumir determinados valores num certo intervalo. Em geral, representam inteiros resultantes do processo de contagem. Exemplo: número de alunos por sala, de acidentes por ano num determinado cruzamento.

b) Qualitativas: quando os elementos da população não são exclusivamente contáveis. Muitas vezes elas podem ser classificadas também segundo algumas de suas características típicas. Nesses casos, as variáveis podem ser agrupadas em nominais ou por postos.

ATIVIDADE II

Fases do levantamento estatístico

Objetivo:

-Verificar as fases de um levantamento estatístico.

A etapa de planejamento de uma pesquisa é fundamental para que os dados coletados possam fornecer informações capazes de responder às nossas indagações. Para tanto, a coleta de dados e sua análise, devem ser feitas de forma criteriosa e objetiva tornando os resultados confiáveis. Os passos a serem seguidos são:

2.1 Definição do Universo

Responder: quem, o que, por que e quando.

Conforme as respostas obtidas serão dadas as coordenadas para o início da pesquisa. O universo a ser investigado deve ser definido precisamente, sob pena de comprometer o resultado do levantamento.

2.2 Decisão sobre o tipo de levantamento

Os fatores tempo, custo e precisão determinam a realização de um levantamento censitário ou amostral.

2.3 Obtenção das informações

Há várias maneiras de se obter informações. Dentre elas: via postal, por telefone, entrevista direta, aplicação de questionário, experimentos e pesquisa em um banco de dados.

2.4 Elaboração do questionário

É obra das mais delicadas, pois é o instrumento que conterá as informações necessárias para alcançar os objetivos da pesquisa.

Algumas medidas aconselhadas para a elaboração do questionário:

- inclusão das possíveis respostas de cada item, ou pelo menos as mais freqüentes;

- as perguntas devem ser formuladas de tal modo que as respostas sejam objetivas e possam ser facilmente apuradas;

- a disposição das perguntas devem apresentar uma seqüência lógica de raciocínio, além de oferecer espaço suficiente para as respostas;

- evitar redações longas para as questões e não utilizar questões ambíguas;

- o questionário não deve ser extenso a fim de não prender o informante durante muito tempo.

Após termos os questionários prontos e os agentes habilitados, é conveniente realizar um levantamento experimental (amostra piloto).

2.4.1 Tipos de questões

Questões de Identificação

Idade ________ Série ______ Gênero: ( ) masculino ( ) feminino

Procedência: _______________________________________________

Questão fechada

a) Assinale qual o destino do lixo/resíduo sólido produzido na sua casa:

( ) Vai para o Lixão (Depósito Municipal de Resíduos Sólidos)

( ) É Reciclado (vendido) ( ) É Queimado ( ) É Reutilizado

( ) Desconhece o destino ( ) É feita a compostagem

b) Classifique as alternativas conforme o grau de produção que você atribui a elas.

(1) Se você achar que é muito produzido

(2) Se você achar que é pouco produzido

(3) Se você achar que é muito pouco produzido

(4) Se você achar que não é produzido

O lixo / resíduo sólido produzido por você em sua residência:

( ) papel ( ) pilhas ( ) plástico ( ) latas ( ) entulho ( ) metais ( ) lâmpadas ( ) madeira ( ) vidro ( ) borracha ( ) resíduos infectantes ( ) borracha ( ) resíduos orgânicos

(restos de alimentos)

Questão semi aberta

Você separa o lixo produzido por você na sua casa?

( ) Sim ( ) Não Porque? ____________________________

Questão aberta

Qual o seu entendimento do que seja Gerenciamento de Resíduos Sólidos/Lixo?

2.5 Codificação dos Dados

Depois de eliminados os boletins de possíveis erros, são os mesmos separados e classificados em grupo para a codificação, contagem e síntese dos resultados. A tal estágio de trabalho estatístico dá-se o nome de apuração, que é realizado de acordo com o volume e natureza do levantamento efetuado, podendo ser realizada de forma manual ou com o uso de computador.

Ex: Armazenamento dos dados

N° Quest	Item do Questionário
N° Quest	Idade	Gênero
1
2
3
4

Para cada uma das questões qualitativas são criados códigos:

Ex: Variável Gênero: 1-Feminino 2-Masculino Obs: No EXCEL Fig. 1

2.6 Apresentação dos Dados

Os dados podem ser sintetizados e apresentados em quadros, tabelas e/ou em forma de gráficos. Devem ser analisados e divulgados.

2.7 Relatório Final

A cada pesquisa deve corresponder um relatório, fazendo uma descrição geral da pesquisa: região geográfica, natureza das informações coletadas, métodos de coleta de dados, de amostragem, finalidade da pesquisa, custo, avaliação, planejamento, precisão, etc.

ATIVIDADE III

Organização de dados

Objetivo: Aplicar métodos estatísticos para análise e interpretação de dados.

Construir tabelas e gráficos

A aplicação dos métodos estatísticos tem como finalidade básica a análise e a interpretação de dados gerados em estudos observacionais ou experimentais. A área da Estatística que trata da organização e do resumo de dados é chamada de Estatística Descritiva. Quanto à organização e descrição dos dados, consiste basicamente na representação dos dados em tabelas e gráficos, bem como na construção de medidas de síntese numérica. Em geral, é aplicada antes de técnicas de análise mais sofisticada, pois, pode contribuir enormemente para a geração de hipóteses sobre o objeto em estudo.

Planilha e Tabela no Excel

Para utilizar planilha do Excel para digitar uma tabela (texto) ou como banco de dados, utilizam-se colunas como variáveis e linhas como registros (indivíduos), conforme a figura 1.

Para numerar seqüencialmente basta digitar 1 e 2, selecionar e arrastar até o número desejado, da mesma forma para datas e outras seqüências.

Figura 1 – Planilha de trabalho do Microsoft EXCEL

3.1 Apresentação Tabular

A apresentação de dados estatísticos na forma tabular consiste na reunião ou agrupamento dos dados em tabelas ou quadros com a finalidade de apresentá-los de modo ordenado, simples e de fácil percepção e com economia de espaço. A tabela deve ser objetiva, mas clara, permitindo que o leitor possa estabelecer relações e tirar conclusões sobre o assunto apresentado.

As tabelas devem ter os seguintes componentes: título, cabeçalho, coluna indicadora, corpo da tabela e rodapé, conforme o exemplo seguinte:

Tabela2: Quantidade de lixo reciclado no Brasil e Estados Unidos–2000

Espécie	Brasil (169,7 milhões de Hab)		USA (278,4 milhões de Hab)
Espécie	Total (em T)	% do Total	Total (em T)	% do Total
Latas de Alumínio	7,4 bilhões⁽¹⁾	78	62,6 bilhões⁽¹⁾	63
Vidro	378 mil	42	2,5 milhões	40
Latas de Aço	300 mil	40	1,5 milhão	58,4
Papel	2,6 milhões	22	47,3 milhões⁽²⁾	45
Plástico	200 mil	15	1,1 milhão⁽²⁾	5,2

Fonte: Cempre, U.S. Environment Protection Agency , Aliminun Association, Steel Recycling, Institute e American Forest & Paper Association.⁽¹⁾Em latas ⁽²⁾Dados de 1999.

Título: precede a tabela e explica, em poucas palavras, o dado em estudo; responde as perguntas “o que está sendo apresentado?”, “onde?” e “quando?” ocorreu ou ocorre o fato.

Cabeçalho: é o local dos informes dos conteúdos de cada coluna.

Coluna indicadora: especifica o conteúdo de cada linha.

Corpo da tabela: apresenta os dados.

Rodapé: é mencionada a fonte dos dados e pode também conter as notas ou chamadas, que são esclarecimentos gerais ou particulares relativos aos dados.

3.1.1 Tabela Simples

Contém somente uma ordem de classificação.

Tabela 3: Produção mundial de etanol (álcool derivado de cana , milho, beterraba,etc.) em 2005.

Fonte	%
Brasil	36,4
EUA	35,5
China	8,2
Índia	3,7
Demais	16,2

Fonte: Unica, ANP e Detagro/F.O.Licht

3.1.2 Tabela de Dupla Entrada

Neste tipo de tabela são criadas duas ordens de classificação. Uma horizontal (linha) e uma vertical (coluna).

Tabela 4: Destino do lixo final (em t/dia)- Brasil - 2000

Região Local	Norte	Nordeste	Sudeste	Sul	Centro-Oeste	Brasil
Aterro controlado	3 133,9	6 071,9	65851,4	4 833,9	4 684,4	84 575,5
Aterro sanitário	1 468,8	15 030,1	52,542,3	8 046,0	5 553,1	82 640,3
Lixão	6 279,0	20 043,5	13755,9	5 112,3	3 131,0	48 321,7
Estação de Compostagem	5,0	74,0	5437,9	347,2	685,6	6 549,7
Estação de triagem	-	92,5	1262,9	832,6	77,0	2 265,0
Locais não fixos	95,6	128,4	781,4	119,9	104,9	1 230,2
Incineração	8,1	22,4	945,2	30,1	26,0	1 031,8
Depositado em áreas alagadas	56,3	45,0	86,6	36,7	8,0	232,6
Outra	20,4	50,0	953,2	516,1	26,5	1 566,2
Total	11 067,1	141 616,8	141 616,8	19 874,8	14 296,5	228 413,0

Fonte: PNSB 2000/IBGE

3.2 Apresentação de dados em tabelas e gráficos no EXCEL

3.2.1 Construção de tabelas simples a partir de dados sistematizados

Título da tabela: deve ser digitado numa única célula.

Corpo da tabela: é composto pela linha do cabeçalho, linhas das categorias e linha do total, esta última opcional.

ª Totais: para totalizar colunas utilize o ícone (auto soma).

ª Percentuais: utilizam-se fórmulas, iniciando pelo sinal de = (igual) e digitando os valores numéricos ou referências nas células onde estão os valores de interesse. Por exemplo, para o cálculo do percentual do sexo feminino na tabela 1 da figura 1:

§posicionar o cursor na célula onde quer o resultado: C4

§digitar o sinal de igual =

§clicar na freqüência absoluta do sexo feminino (célula B4)

§digitar o sinal de divisão /

§clicar no valor total (célula B6)

§digitar o sinal da multiplicação *

§digitar 100

§teclar <enter>

ª Fonte: digitar o texto referente a fonte. O tamanho da letra deve ser menor que a do corpo da tabela.

ª Bordas: selecionar as células para introduzir bordas. No menu formatar, escolher a opção célula e fixa a borda conforme figura 2.

Texto explicativo 3: Ícones indicando a localização da borda

Figura 2 – Formatar bordas

3.2.2 Construção de tabelas simples e gráficos a partir de um banco de dados

Escolhe-se a opção “Relatório de tabela e gráfico dinâmico” no menu Dados, sendo apresentada a tela da figura 3.

Como padrão está selecionada a opção de tabela dinâmica, caso deseja-se um gráfico, deve-se selecionar a segunda opção, conforme figura 3. Após, selecionar <avançar>, sendo apresentada a tela conforme figura 4, na qual seleciona-se o banco de dados, com o mouse pressionado ou <SHIFT> + <setas>.

Quando é apresentada a tela da figura 5, seleciona-se o local da planilha onde quer apresentar o resultado, optando por uma célula da planilha atual ou uma nova planilha. Após, clicar no botão Layout.

Neste momento escolhe-se o modo de apresentação da tabela (layout), apresentada na figura 6. Para escolher o local de apresentação das categorias da variável, deve-se arrastar o botão referente a variável apresentada a direita da tela até o corpo da tabela, apresentada no centro da tela sobre LINHA ou COLUNA. Em seguida, arrasta-se novamente o botão da variável para o centro do corpo da tabela para calcular freqüência absoluta, ou seja, contar as categorias. Deve aparecer no botão: Contar de nome_da_variável, por exemplo: . Caso isso não ocorra, clicar duplo sobre o botão e escolher a opção ContNúm.

Para calcular a freqüência relativa percentual, deve-se novamente arrastar o botão da variável até o centro do corpo da tabela e clicar duplo sobre o botão, sendo apresentada a tela da figura 7, clica-se em Opções e no campo Mostrar dados como, seleciona-se a opção: % de coluna e < OK >.

Clicando no botão OK e no botão Concluir aparecerá a tabela dinâmica da Figura 8.

Figura 8 – Exemplo de tabela simples dinâmica

O processo para a construção do gráfico dinâmico é o mesmo, desde que seja selecionada a opção “Relatório de gráfico dinâmico” na figura 3.

3.3 Construção de tabelas cruzadas a partir de um banco de dados

O processo para a construção de tabelas cruzadas dinâmicas é igual a construção de tabelas simples, selecionando-se mais uma variável para o corpo da tabela conforme a figura 9, colocando-a sobre a COLUNA. Finalizando todo o processo aparecerá a tabela cruzada conforme figura 10.

Figura 9 – Tabela cruzada

Figura 10 – Exemplo de tabela cruzada dinâmica

3.4 Representação gráfica

3.4.2 Princípios Básicos na Construção de Gráficos

Depois de sintetizados em tabelas, os dados podem ser apresentados em gráfico, a fim de proporcionarem ao interessado uma visão rápida do comportamento do fenômeno.

Requisitos Fundamentais:

-Simplicidade (Sem traços desnecessários)

-Clareza (para uma correta interpretação)

-Veracidade.

3.4.2 Elementos dos Gráficos

Título: localizado acima ou abaixo do gráfico, informa sobre o que está sendo apresentado. Deve ser simples, claro e objetivo.

Escala: no eixo das abscissas (x) cresce da esquerda para a direita e é escrita embaixo do eixo. No eixo das ordenadas (y) cresce de baixo para cima e é escrita à esquerda.

Variáveis: o nome da variável deve ser centralizado e colocado no eixo das abscissas embaixo da escala, no eixo das ordenadas na extremidade.

Traçado: o sistema de eixos cartesianos e as linhas auxiliares devem ser traçados mais leves do que a linha demonstrativa.

Fonte: localizada no rodapé do gráfico, indica o responsável pelo fornecimento dos dados.

Opcionais: Setas: podem ser feitas para indicar a direção dos eixos.

Notas: idêntico à das tabelas

3.4.3 Tipos de Gráficos

Os dados sistematizados podem ser apresentados em gráficos, estes atraem mais a atenção do leitor e auxilia no sentido de apresentar figuras (barras, colunas,..) para representar a quantidade de cada categoria. Existem diferentes tipos de gráficos, os quais são mais adequados para cada tipo de variável e representam uma ou duas variáveis. A seguir são apresentados os tipos de gráficos mais usados.

a)Gráfico em Setores

É usado para representar uma variável aleatória, sendo que suas categorias devem totalizar 100%.

Primeiramente, selecionam-se as categorias e os valores absolutos ou relativos que serão apresentados no gráfico.

Após, para construir um gráfico de setores deve-se clicar no ícone na barra de ferramentas ou no menu Inserir, escolhe-se a opção Figura e então Gráfico. Neste momento aparecerá a tela referente ao Assistente Gráfico, como apresentada na figura 14. Escolhendo o Tipo de gráfico Pizza aparecerá subtipos de gráficos, podendo-se escolher um dos 6 tipos e então clicar no botão Avançar.

Utilizando como exemplo a tabela 5 da figura 11, será apresentada a figura 13 (etapa 2), na qual é apresentada uma prévia do gráfico escolhido.

Figura 11 – Tabela 5

Figura 12 – Gráfico de setores – etapa 1

Na etapa 3 (figura 14), clicar no campo Título do gráfico e digitar o título do gráfico. Após, clicar na ficha Legenda (figura 15) para alterar o local de posição da legenda ou para excluí-la. Na ficha Rótulos de Dados é possível mostrar o nome das categorias e a percentagem conforme figura 16. Após, deve-se clicar no botão Concluir.

Figura 13 – Gráfico de setores – etapa 2

Figura 16 – Gráfico de setores – etapa 3, rótulos de dados

A figura 17 apresenta o gráfico exemplo da tabela 01 (figura 1). Para incluir a fonte utiliza-se a barra de Ferramentas Figura da seguinte maneira (caso não esteja ativa):

menu Exibir;

opção Barra de Ferramentas;

opção Desenho

Então, a Barra de Ferramentas Desenho aparecerá na parte inferior da planilha, nela clicar no ícone referente a Caixa de Texto, clica-se no local onde quer que apareça a fonte do gráfico e então digita-se a fonte.

Pode-se personalizar o gráfico, alterando a cor dos setores, alternado a cor do fundo, alterando o tamanho, tipo e cor da fonte.

Para alterar a cor dos setores, deve-se clicar uma vez no gráfico, clicar mais uma vez no setor que deseja alterar a cor e, em seguida efetuar um clique duplo para aparecer o menu de cores. Então, seleciona-se uma cor ou no botão Efeitos de Preenchimento para utilizar as opções gradiente ou textura.

Figura 17 – Gráfico de setores - exemplo

O gráfico de setores é indicado quando o número de categorias são no máximo 5.

b)Gráficos de colunas ou barras simples

São utilizados para representar uma variável aleatória. O procedimento é o mesmo utilizado no gráfico de setores, sendo que na etapa 3 (figura 18) digita-se além do título do gráfico, o título do eixo x e o título do eixo y.

Figura 18 – Gráfico de colunas – etapa 3

O gráfico para a tabela 1 da figura 1 está apresentado na figura 19.

Figura 19 – Gráfico de colunas – exemplo

Um exemplo do gráfico de barras é apresentado na figura 20, sendo sua construção idêntica ao gráfico de colunas.

Figura 20 – Gráfico de barras – exemplo

c) Gráficos de colunas ou barras agrupadas

São utilizados para representar duas variáveis aleatórias (tabela cruzada). Inicialmente, selecionam-se as categorias das duas variáveis e as freqüências absolutas ou relativas, como apresentado na figura 21e 22. Clicando no ícone , aparecerá a figura 14, onde escolhe-se gráfico de barras ou colunas, procedendo da mesma maneira que no anterior.

Figura 21 – Gráfico de Colunas Agrupadas – seleção dos dados

Figura 22 – Gráfico de Barras Agrupadas – seleção dos dados

d) Gráfico de linhas

É utilizado para representar uma série temporal, ou seja, uma série de dados coletados ao longo do tempo, em segundo, horas, dias, anos,.. Primeiramente, selecionam-se os dados – referente ao tempo - e os valores, como no exemplo apresentado na figura 23, procedendo conforme já visto nos outros tipos de gráficos.

Figura 23 – Gráfico de Linha – seleção dos dados

Pode-se personalizar o gráfico, alterando a escala, cor da linha, do fundo,.. Para alterar a escala no eixo y (eixo vertical), deve-se clicar duplo sobre o eixo e escolher a ficha Escala. Para alterar a cor da linha e espessura, clicar duplo sobre a linha.

Um gráfico personalizado para apresentar os valores em reais da Cesta Básica de Santa Rosa no ano de 2002 é apresentado na figura 24.

Figura 24 – Gráfico de Linha – exemplo

Lembre-se da importância de uma escala corretanos gráficos e o seu formato, sendo que o eixo y (vertical) representa ± 80% do eixo x (horizontal). Também, a inclusão de título e fonte no gráfico e o título dos eixos.

Existem outros tipos de gráficos, utilizados em situações mais específicas, sendo o procedimento semelhante ao apresentado neste material.

ATIVIDADE IV

Sintetização e análise de dados estatísticos quantitativos.

Objetivo:

-Definir e operacionalizar as principais estatísticas para dados quantitativos

4.1 Análise de Dados Estatísticos Quantitativos.

4.1.1 Sintetização e Análise de Dados Não Agrupados. ( n<20)

Quando os dados coletados forem menores que 20, numa relação de um a um, no formato de série numérica, devemos trabalhar da seguinte forma:

Exemplo: Número de professores por escola. Cidade X -2005.

X_i= 45-27-19-19-36-52

Rol: arranjar os dados brutos em ordem crescente.

Ex: rol = 19-19-27-36-45-52

Medidas de Tendência Central

Os valores que em estatística caracterizam os valores médios são chamados de medidas de tendência central. Entre as principais, destacam-se a média aritmética, a moda e a mediana.

a)Média Aritmética.

É a medida de tendência central definida como o quociente entre a soma de todos os valores da variável e o número de elementos desta.

onde n é o número de termos do conjunto X₁, X₂,..,X_n.

Propriedades da média aritmética:

- A soma algébrica dos desvios de um conjunto de valores em relação à média aritmética é zero.

- A soma algébrica dos quadrados dos desvios de um conjunto de valores em relação à média aritmética é mínima.

- Somando-se ou subtraindo-se uma constante a todos os valores de uma variável, a média ficará acrescida ou subtraída dessa constante.

- Multiplicando-se ou dividindo-se todos os valores de uma variável por uma constante, a média ficará multiplicada ou dividida por essa constante.

Vantagens do uso da média aritmética:

- Pode ser determinada com precisão matemática, sendo que, faz uso de todos os dados para o seu cálculo.

- Pode ser determinada quando somente o valor total e o número de elementos forem conhecidos.

Desvantagens do uso da média aritmética:

- Não pode ser empregada para dados qualitativos.

- É influenciada por valores extremos, podendo em alguns casos, não representar a série.

Ex=

Em média estão lotados 33 professores por escola na cidade X em de 2005.

b) Moda

Como o próprio nome indica, é o valor que ocorre com maior freqüência em um conjunto de valores. As distribuições que apresentam uma moda única são chamadas de unimodais. Quando apresentam duas modas, bimodais e três ou mais modas, plurimodal. São chamadas de amodais as distribuições que não apresentam nenhuma moda.

Vantagens do uso da moda:

- É de uso prático.

- A moda geralmente é um valor verdadeiro e por conseguinte, pode mostrar- se mais real e coerente.

Desvantagens do uso da moda:

- Não inclui todos os valores de uma distribuição.

- Mostra-se ineficiente quando a distribuição é largamente dispersa.

Ex: Na nossa análise a moda é 19. O número de professores lotados por escola que ocorrem com maior freqüência é de 19

c)Mediana

A mediana é o valor central da distribuição, ou seja que divide o conjunto de dados em duas partes de freqüências iguais.

Considere para o cálculo da mediana (quando a variável em estudo é discreta):

-Se n (número de termos) é ímpar, o valor da mediana será o valor da variável que ocupa o posição de ordem

-Se n (número de termos) é par, nesse caso, não existe no conjunto ordenado um valor que ocupe o valor central, isto é, a mediana será determinada pela média aritmética dos valores que ocupam a posição de ordem .

Ex: Na nossa análise o n é 6 , logo a posição é:

50% do número de professores lotados por escola em 2005 estão abaixo de 31,5 e 50% acima.

Medidas de Dispersão ou variabilidade

Freqüentemente não é suficiente usar apenas uma medida de posição para interpretar adequadamente um conjunto de dados. Assim, juntamente com uma medida de tendência central é desejável dispor de uma medida de dispersão dos dados, através do qual é possível quantificar a variabilidade em relação ao centro da distribuição.

Logo, medidas de dispersão são medidas utilizadas para avaliar o grau de variabilidade dos valores de uma variável em torno da média, ou seja, são medidas que servem para avaliar a representatividade da média.

a)Amplitude Total

É a diferença entre o valor mais alto e o mais baixo dos valores de uma distribuição. Como depende apenas dos valores extremos, ou seja, não depende dos valores internos, seu uso torna-se muito limitado.

At = Ls – Li (limite superior menos limite inferior) Ex: At = 52-19= 33

b)Variância

Variância de um conjunto de dados (s²) é a média aritmética dos quadrados dos desvios.

Propriedades da variância:

- A variância de uma constante é nula.

- Somando-se ou subtraindo-se uma constante a todos os valores de uma variável, a variância dessa variável não se altera.

- Multiplicando-se ou dividindo-se todos os valores de uma variável por uma constante, a variância ficará multiplicada ou dividida pelo quadrado dessa constante.

c)Desvio Padrão

É a raiz quadrada da variância, expressa na mesma unidade de medida dos dados. O desvio padrão é uma medida que permite estimar o “erro”, isto é a variação não controlada, ao acaso.

Podemos dizer que:

- Quanto menor for o desvio padrão, mais aproximado estão os valores da variável de sua média;

- Se o desvio padrão for zero, então todos os valores da variável são iguais;

- Se o desvio padrão for grande, os valores da variável estão muito afastados de sua média.

Ex: Para calcular o desvio padrão do nosso grupo de informações, devemos proceder da seguinte forma:

X_i

( X_i - )

( X_i - )²

-6

-14

144

196

361

942

d)Coeficiente de variação

Trata-se de uma medida relativa de dispersão útil para a comparação do grau de concentração em torno da média de séries distintas.

(geralmente expressa em porcentagem)

A quantidade CV, é um número abstrato, ou seja, independe das unidades de medidas(m, km,%, ,etc). Ele representa o desvio padrão que seria obtido se a média fosse igual a 100.

Na prática podemos dizer:

CV£ 30 ® O conjunto de dados é um grupo homogêneo em relação a média

Até 10% ®a media é considerada um ótimo representante para os dados.

De 11% a 20% ®a média é considerada um bom representante para os dados.

De 21% a 30% ®a média é considerada um representante regular para os dados.

CV>30® O conjunto de dados é um grupo heterogêneo em relação a média.

Ex: CV= 13,72/33 = 0,4157 x 100 = 41,57% ® Grupo heterogêneo, a média não é um bom representante para este conjunto de dados.

4.1.2 Sintetização e Análise de Dados Agrupados. ( n≥20)

As técnicas de sistematizar dados quantitativos, quando o tamanho do conjunto de dados é igual ou superior a 20 são: tabela de freqüência, histograma(gráfico) ou polígono de freqüência(gráfico).

A construção da tabela de distribuição de freqüência consiste essencialmente em colocar os dados agrupados, distribuídos em classes, cujo tamanho e número deverá ser previamente calculado lembrando sempre que o objetivo básico é resumir os dados com perda mínima de informações. O primeiro passo é determinar o tamanho e o número de classes através da aplicação do seguinte cálculo:

, onde: h_i é a amplitude do intervalo

n é o tamanho da amostra.

é número de intervalos

Pode-se aproximar o valor de h_i para um valor próximo com um menor número de casas decimais ou em inteiros. Após constrói-se a tabela, colocando no primeiro intervalo o valor inferior do conjunto de dados mais o valor do h_i. No segundo intervalo como limite inferior coloca-se o limite superior do intervalo anterior e como limite superior, soma-se o mesmo com o h_i. E assim sucessivamente.Exemplo: h_i.= 4

Tabela 6 – Distribuição de freqüências das idades dos 50 professores da Escola X. Porto Alegre-RS-2005

Valores de Xi

fr%

22|---- 26

26|---- 30

Total

---

1,00

100

---

Fonte:Dados fictícios.

Onde:

- fi: freqüência absolutasimples.

- fr: freqüência relativa

-fa: freqüência absoluta acumulada. F

-fr%: freqüência relativa percentual

-x_i: ponto médio dos intervalos.

4.1.3 Medidas descritivas para dados agrupados

Quando se tem uma distribuição de freqüência, aos dados agrupados para calcular as medidas descritivas deve-se acrescentar na tabela os valores e .

Tabela 7 –Distribuição de freqüências das idades dos 50 professores da Escola X.Porto Alegre-RS-2005

Valores de Xi

22|---- 66

26|---- 30

Total

---

Fonte:Dados fictícios.

As fórmulas para as medidas são:

a)Média Aritmética:

b)Mediana:

Onde: p= posição do termo mediano:

l_i= limite inferior do intervalo mediano

= freqüência acumulada anterior ao intervalo mediano

= freqüência absoluta do intervalo mediano

c)Moda: Intervalo modal é o intervalo de maior freqüência absoluta.

Onde:

d₁=freqüência absoluta maior, menos a freqüência absoluta anterior

d₂=freqüência absoluta maior, menos a freqüência absoluta posterior

d)Variância ou

e) Desvio Padrão

f)Coeficiente de variação

g)Região de normalidade

ATIVIDADE V

Estatística descritiva utilizando o excel

Objetivo: Definir estatísticas descritivas no excel

O EXCEL disponibiliza uma ferramenta de análise de dados para cálculos estatísticos mais complexos. Para utilizá-la é necessário instalá-la clicando no menu Ferramentas, depois em Suplementos e então selecionar Ferramentas de Análise conforme a figura 25.

A partir deste momento, a opção Análise de Dados estará disponível no menu Ferramentas, conforme figura 26.

Figura 25 – Instalação das Ferramentas de Análise

Figura 26 – Ferramentas de Análise

Para calcular as estatísticas descritivas utilizando as Ferramentas de Análise de Dados, clicar em Estatística Descritiva e no botão OK, conforme indicado pela seta na figura 26.

Quando aparecer a tela apresentada na figura 27, selecionam-se os dados, a opção de saída – nova planilha ou intervalo de saída - e seleciona-se a opção Resumo Estatístico.

Se for selecionado o nome da variável junto com os dados, deve-se selecionar a opção Rótulos na primeira linha.

O resultado da Análise de Dados – Estatística Descritiva para o exemplo da figura 1, referente a variável idade é apresentado na figura 28.

Figura 27 – Estatística descritiva nas ferramentas de análise

Figura 28 – Resultado da Estatística Descritiva – Ferramentas de Análise de Dados

ATIVIDADES À DISTÂNCIA

a)Elaborar um questionário que envolva um tema possível de se explorar no Ensino Médio.

b)Aplicar o questionário elaborado sobre o tema na escola em que trabalha.

c) Codificar os dados, apresentando-os em tabelas e gráficos.

d) Com uma das medidas quantitativas da pesquisa calcular as medidas de tendência central e de dispersão.

e) Apresentação em seminário.

Atendimento On-line programado para Estatística

Endereço para acesso: http://www.projetos.unijui.edu.br/matematica/rosane

Turma A: Dia 12/05/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia 12/05/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 12/05/2006 no turno da noite das 18h:00mim até 22h:00min

Atendimento em Estatística por mensagens em qualquer horário

Para tirar dúvidas sobre este trabalho,através de mensagens acesse o seguinte endereço: http://www.projetos.unijui.edu.br/matematica/rosane e clique em deixe seu recado.

O último endereço informado acima funciona 24 horas por dia para recados. Se for colocado o E-mail de quem acessar será dado retorno para o E-mail informado dentro 72h.

BIBLIOGRAFIA

Microsoft EXCEL 2002.

BATTISTI, I. E.; Kirchner, R. M.; Fricke R. M. Rotinas da Planilha Eletrônica

EXCEL para Uso em Estatística Descritiva. (Cadernos UNIJUÍ) Ijuí: UNIJUÍ, 2003

BUSSAB, W. O.;MORITTIN P. Estatística Básica. São Paulo: Saraiva, 2003.

TRIOLA, M. Introdução à Estatística. Rio de Janeiro: Ed. LTC, 1999.

VEIGA, R.; FERREIRA, D.; SÁFADI,T.; LIMA, P. Técnicas Computacionais Aplicada à Matemática e à Estatística. Lavras. MG: UFLA. 2000.

Anexos

Cronograma das aulas nos momentos presenciais e à distância, formas de comunicação e formas interação durante as atividades à distância

Primeira etapa-Presencial

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma A

27/03/2006

28/03/2006

29/03/2006

30/03/2006

31/03/2006

Recepção aos Professores

.Palestra 01: Formação do Professor Hoje.

Profº Dr. Otávio Aloisio Maldaner

Palestra 02: Organização do Currículo Escolar

Profª Drª Lenir Basso Zanon e Profª Dr. Milton Auth

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Estatística

Profª Drª Rosane Maria Kirchner

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

* 2º parte de Seminários-Situação de estudo

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma B

27/03/2006

28/03/2006

29/03/2006

30/03/2006

31/03/2006

Recepção aos Professores

.Palestra 01: Formação do Professor Hoje.

Profº Dr. Otávio Aloisio Maldaner

Palestra 02: Organização do Currículo Escolar

Profª Drª Lenir Basso Zanon e Profª Dr. Milton Auth

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Informática*

Profª Msc Tânia Michel Pereira

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

* 2º parte de Seminários-Situação de estudo

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma C

27/03/2006

28/03/2006

29/03/2006

30/03/2006

31/03/2006

Recepção aos Professores

.Palestra 01: Formação do Professor Hoje.

Profº Dr. Otávio Aloisio Maldaner

Palestra 02: Organização do Currículo Escolar

Profª Drª Lenir Basso Zanon e Profª Dr. Milton Auth

Informática*

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Modelagem

Profª Msc Denise Knorst da Silva

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

* 2º parte de Seminários-Situação de estudo

Segunda etapa – à Distância

Cronograma de atendimento Programado do Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma A

2ª-feira - 11/04/2006

4ª-feira- 19/04/2006

6ª-feira-12/05/2006

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Cronograma de atendimento Programado do Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma B

2ª-feira - 11/04/2006

4ª-feira- 19/04/2006

6ª-feira-12/05/2006

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Cronograma de atendimento Programado do Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma C

2ª-feira - 11/04/2006

4ª-feira- 19/04/2006

6ª-feira-12/05/2006

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Terceira etapa – Presencial

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma A

22/05/2006

23/05/2006

24/05/2006

25/05/2006

26/05/2006

Modelagem

Profª Msc Denise Knorst da Silva

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Seminário por componente para apresentação dos trabalhos.

Informática

Profª Msc Tânia Michel Pereira

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Continuação seminário

(2 horas)

_________________

Avaliação dos trabalhos

(2 horas)

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma B

22/05/2006

23/05/2006

24/05/2006

25/05/2006

26/05/2006

Estatística

Profª Drª Rosane Maria Kirchner

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Seminário por componente para apresentação dos trabalhos.

Modelagem

Profª Msc Denise Knorst da Silva

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Continuação seminário

(2 horas)

_________________

Avaliação dos trabalhos

(2 horas)

Cronograma de Atividades Curso de Capacitação de Professores de Matemática do Ensino Médio - Turma C

22/05/2006

23/05/2006

24/05/2006

25/05/2006

26/05/2006

Informática

Profª Msc Tânia Michel Pereira

Informática

Profª Msc Tânia Michel Pereira

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Seminário por componente para apresentação dos trabalhos.

Estatística

Profª Drª Rosane Maria Kirchner

Estatística

Profª Drª Rosane Maria Kirchner

Modelagem

Profª Msc Denise Knorst da Silva

Informática

Profª Msc Tânia Michel Pereira

Continuação seminário

(2 horas)

_________________

Avaliação dos trabalhos

(2 horas)

formas de comunicação e formas interação durante as atividades à distância

Ambiente específico do curso interligado com o ambiente AMEM e Atendimento On-line do DeFEM

Endereço para acesso ao ambiente: http://www.projetos.unijui.edu.br/matematica/ccpmem qual estará disponível de 27 de março de 2006 a 30 de dezembro de 2006 para acesso. Todas as informações sobre o funcionamento deste ambiente poderão ser obtidas a partir da primeira página deste endereço.

É de responsabilidade da professora Tânia Michel Pereira durante as aulas presenciais do tema Informática no Ensino da Matemática a interação com todos os recursos deste ambiente no primeiro período presencial. Neste os alunos terão acesso:

· ao atendimento On line da Secretaria do departamento;.

· aos fóruns propostos pelos professores do curso (acesso mediante senha);

· aos "chats" ou bate-papos agendados por alunos (acesso mediante senha);

· ao recurso de envio e recebimento de mensagens (acesso com senha);

· às páginas dos docentes do curso;

· às páginas dos professores/alunos do curso;

· aos links para acesso a diversos Materiais didático virtual para ensino da matemática na Educação Básica

Outras opções de interação disponíveis

E-mail: defem@unijui.tche.br

Telefone ou Fax:

· Telefone 55 3332 0229;

· Fax 55 3332 0900

Endereço para correspondência:

· DeFEM /Curso de Capacitação dos Professores de Matemática do Ensino Médio, Rua São Francisco, nº 501. Bairro São Geraldo - Ijuí – RS. CEP 9870-000

Atendimento na sede da instituição:

Sala 510 da Sede Acadêmica – Rua São Francisco, 501. Bairro São Geraldo- Ijuí – RS através agendamento antecipado via telefone, e-mail, atendimento on-line, a pedido dos alunos.

Horários programado para Atendimento On-line dos Professores de Matemática do Curso

Atendimento On-line para Seminários de Situação de Estudo

http://www.projetos.unijui.edu.br/gipec

Distribuído da seguinte forma

Turmas A, B e C: Dia 25/04/2006 no turno da tarde das 13h:30mim até 17h:30min

Atendimento On-line para Modelagem

http://www.projetos.unijui.edu.br/matematica/denise

Distribuído da seguinte forma

Turma A: Dia 11/04/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia 11/04/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 11/04/2006 no turno da noite das 18h:00mim até 22h:00min

O endereço informado acima funciona 24 horas por dia para recados. Se for colocado o E-mail de quem acessar será dado retorno para o E-mail informado dentro de 24h

Atendimento On-line para Matemática e Informática na Educação Matemática

Para tirar dúvidas sobre este trabalho, entre no atendimento On-line pelo seguinte endereço:

http://www.projetos.unijui.edu.br/matematica/tania O atendimento está organizado da seguinte forma:

Turma A: Dia 19/04/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia 19/04/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 19/04/2006 no turno da noite das 18h:00mim até 22h:00min

O endereço informado acima funciona 24 horas por dia para recados. Se for colocado o E-mail de quem acessar será dado retorno para o E-mail informado pelo aluno, dentro de 72h

Atendimento On-line para Estatística

Para tirar dúvidas sobre este trabalho, entre no atendimento On-line pelo seguinte endereço:

http://www.projetos.unijui.edu.br/matematica/rosane O atendimento está organizado da seguinte forma:

Turma A: Dia 12/05/2006 no turno da manhã das 7h:50mim até 11h:50min

Turma B: Dia 12/05/2006 no turno da tarde das 13h:30mim até 17h:30min

Turma C: Dia 12/05/2006 no turno da noite das 18h:00mim até 22h:00min

O endereço informado acima funciona 24 horas por dia para recados. Se for colocado o E-mail de quem acessar será dado retorno para o E-mail informado pelo aluno dentro de 72h.

[1] Re-elaboração a partir de texto anterior “ORGANIZAÇÃO DO ENSINO MÉDIO – ÁREA DE CIÊNCIAS E TECNOLOGIA – DESENVOLVIMENTO DE UMA SITUAÇÃO DE ESTUDO”, Autoria de membros do Gipec-Unijuí, 2000, Apresentado no XX EDEQ, PUCRS.

[2] MORTIMER, Eduardo Fleury. Linguagem e Formação de Conceitos no Ensino de Ciências. Belo Horizonte, Ed. UFMG, 2000.

[3] VIGOTSKI, Lev S. A Construção do Pensamento e da Linguagem. Martins Fontes, São Paulo, 2001.

[4] Graduada em Matemática-Licenciatura, Mestre em Matemática e Especialização em: Matemática; Ensino de Ciências e Matemática; Ciências da Computação;Redes de computadores.

[5] Graduada em Matemática, Mestre em Modelagem Matemática.

[6] BARBOSA, J.C. Modelagem Matemática: O que é? Por que? Como? Veritati, n.4, p. 73-80. 2004.

Veja texto na íntegra no endereço http://joneicb.sites.uol.com.br/publi.html.

[7] As informações específicas contidas neste item foram extraídas de:

HISTÓRIA DO GNV. Disponível em: <http://www.brunoautoeletrico.com.br/gnv.htm> Acesso em: 04 de jan. 2006.

[8] [8] A situação ilustrada foi extraída de duas fontes específicas que tratam do tema:

ALMEIDA, L. M. W.. Modelagem Matemática e Formação de Professores. In: V ANPEd- SUL, 2004, Curitiba. Anais do V Seminário de Pesquisa em Educação da Região Sul. Curitiba: Universidade Católica do Paraná, 2004.

BARBOSA, J.C. Modelagem Matemática em Cursos para Não-Matemáticos. In: CURY, H. N. Disciplinas matemáticas em Cursos Superiors: reflexões, relatos, propostas. Porto Alegre: EDIPUCRS, 2004.

[9] Segundo Barbosa (2004), no caso 1 para implementação da modelagem, o professor apresenta um problema, com seus dados qualitativos e quantitativos, cabendo aos alunos a resolução.

[10] PONTE, J. P.; BROCARDO, J; OLIVEIRA, H. Investigações Matemáticas na Sala de Aula. Belo Horizonte: Autêntica, 2003.

[11] Graduada em Matemática , Especialista em Matemática, Mestre em Métodos Quantitativos e Doutora Engenharia Elétrica - Métodos de Apóio a Decisão