Ministério da Educação
Fundo Nacional de Desenvolvimento da Educação
Diretoria de Programas Especiais
Secretaria da Educação do Estado do Rio Grande do Sul
Universidade Regional do Noroeste do Estado do Rio Grande do Sul
Departamento de Física, Estatística e Matemática
Programa de Melhoria e Expansão do Ensino Médio
Curso de Capacitação dos Professores de Matemática do Ensino Médio
TRABALHO DE MODELAGEM
NOME: Sandra Regina Leal Balzan
MATEMÁTICA - TURMA C
ESCOLA: Colégio Estadual Pe. Colbachini
CIDADE: Nova Bassano - RS
PROFESSORA: Denise Knorst da Silva
DATA: Maio/2006
TEMA: A bola de Futebol
JUSTIFICATIVA:
Ao escolher o tema do meu trabalho, pensei em algo que fosse atual e despertasse interesse aos meus alunos.
Através de um levantamento de dados foi comprovado que dos 33 alunos das turmas 301 e 302, 72,73% tem como preferência esportiva o futebol, independente do sexo, pois a maioria é do sexo feminino. Como o futebol é a Paixão Nacional, e aproveitando o ano da copa, escolhi esse tema (A bola de Futebol), pois coincide com o conteúdo que estou abordando para os alunos dos 3ºs anos do ensino médio que é a Geometria Espacial, especificando a esfera.
UM POUCO DE HISTÓRIA:
A bola de Futebol: Matemática e bola tem tudo a ver, a começar pela própria forma do objeto do qual está se falando. Já imaginou jogar futebol com uma bola quadrada? A bola ou esfera é a única forma geométrica que pode ser rolada em qualquer direção. È muito mais fácil rolar um objeto do que arrastá-lo. Pode-se dizer que a bola é uma figura simétrica, pois é igual vista em qualquer posição. Por não se precisar escolher lado ou lugar para bater, ela é o objeto ideal para jogar não só futebol, mas a maioria dos esportes. As bolas são de tamanhos e materiais apropriados para cada esporte.
INVESTIGAÇÃO:
Devido às exigências por parte das confederações mundiais do esporte, as bolas oficiais devem seguir um rigoroso padrão de qualidade. Quanto ao futebol, a FIFA determina o peso, a pressão e a circunferência para cada modalidade e categoria, mas não determina a quantidade nem o formato dos gomos. Para um maior aproveitamento do material utilizado na confecção dessas bolas foi necessário fazer uso da geometria bem como usar de todo o conhecimento matemático para chegar às formas de gomos que se encaixam de maneira a aproveitar o máximo do material utilizado.
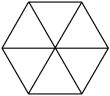
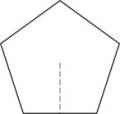
A bola de futebol usada atualmente é a de 32 gomos, sendo composta de 20 hexágonos e 12 pentágonos, porque são as figuras que têm melhor forma de encaixe para formar a bola redonda e o formato mais econômico para o corte dos gomos.
PROBLEMATIZAÇÃO:
Problema 1: Sabendo que as figuras geométricas (pentágonos e hexágonos) que são utilizadas na fabricação de uma bola de futebol são retiradas de uma lâmina de material sintético retangular com dimensões de 1,20 m x 90 cm, e que de uma lâmina são retirados só hexágonos de lado 4,5 cm e de outra só pentágonos de lados com mesma medida, qual a quantidade de hexágonos e pentágonos são retirados de cada lâmina?
Problema 2: Qual o percentual de perda de material de cada lâmina?
Problema 3: Quantas bolas podem ser feitas utilizando a quantidade de recortes de uma lâmina de pentágono e uma de hexágono? Quantas figuras geométricas sobram em cada lâmina?
Problema 4: Qual será a superfície esférica da bola considerando que os hexágonos e pentágonos possuem 4,5 cm de lado?
Problema 5: Qual o diâmetro da bola?
RESOLUÇÃO:
- Cálculo da área da lâmina:
![]()
90 cm
1,20 m
S = base x altura
![]() S
= 1,2 m x 0,9 m = 1,08 m² = 10 800 cm²
S
= 1,2 m x 0,9 m = 1,08 m² = 10 800 cm²
- Cálculo da área do hexágono:
l = 4,5 cm
S = 6. l² Ö3 Considerando Ö3 =
1,73 , temos:
4
S = 6 . (4,5)² . 1,73 = 52,55 cm²
4
- Cálculo da área do
pentágono:
l = 4,5 cm
Partindo do princípio de que a soma dos ângulos
internos de um polígono se calcula pela fórmula:
S = ( n – 2) . 180°
Conclui-se que a soma dos ângulos internos de um pentágono é 540°, logo cada ângulo interno medirá 108°.
Cálculo da altura h:
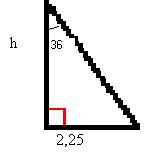
tg 36° = 2,25
h
0,7265 = 2,25
h
h @ 3,10
S = 5 x área do triângulo
S = 5 x 4,5 x h = 5 x 4,5
x 3,1 @ 34,88 cm²
2 2
Problema 1:
1 hexágono ------ 52,55 cm²
x ------ 10 800 cm²
x @ 205,52
l pentágono ------ 34,88 cm²
x ------ 10 800 cm²
x @ 309,63
Logo: De uma lâmina sai 205 hexágonos e de outra lâmina sai 309 pentágonos.
Problema 2:
Hexágono: Pentágono:
10 800 ----- 100% 10 800 ------ 100%
27,25 ----- x 22,08 ------ x
x @ 0,25% x @ 0,2%
Logo: Da lâmina onde são recortados só hexágonos tem 0,25% de perda de material e da lâmina onde são recortados só pentágonos há 0,2% de perda.
Problema 3:
Hexágono: 205 : 20 = 10,25
Pentágono: 309 : 12 = 25,75
Conclui-se que de uma lâmina de hexágonos e de outra de pentágonos pode-se fabricar 10 bolas e sobram 5 hexágonos e 189 pentágonos que poderão ser aproveitadas com as sobras de outras lâminas.
Problema 4:
20 x 52,55 = 1 051
12 x 34,88 = 418,56
Logo a superfície esférica será: 1 051 + 418,56 = 1 469,56 cm²
Problema 5:
Como a área da superfície esférica é: S = 4 p r² temos:
1 469,56 cm² = 4 x 3,14 x r²
1 469,56 cm² = 12,56 r²
1 469,56 cm² = r²
12,56
r @ 10,82
Logo o diâmetro será: 10,82 x 2 @ 21,64 cm.
DISCUSSÃO DOS RESULTADOS:
Levando em consideração que os gomos da bola sejam colados e não costurados, os alunos observaram que com um simples tema (bola de futebol), puderam além de estudar a esfera, rever vários conteúdos como áreas de figuras planas, porcentagem, regra de três, soma dos ângulos internos de um polígono e até trigonometria para descobrir a área do pentágono.
Concluíram também que é preciso dominar tanto a matemática quanto a geometria para se chegar a cálculos precisos e se obter economia na confecção de uma bola de futebol.