UNIJUÍ

Universidade Regional do Noroeste do Estado do Rio Grande do Sul

DEFEM – Departamento de Física, Estatística e Matemática

Adão Reinaldo Vasconcelos Alves

Marlene Brum Guazina

Pelotas, maio de 2006

INTRODUÇÃO

A proposta deste trabalho é discutir o cálculo de área com utilização de material de grande atração por parte dos alunos e muito presente no seu dia-a-dia.Este estudo envolveu os professores Adão Reinaldo Vasconcelos Alves e Marlene Brum Guazina do Ensino Médio da Rede Pública Estadual e vinte alunos da terceira série,noturno, da Escola Técnica Estadual Profª Sylvia Mello localizada no bairro Fragata, à rua Evaristo da Veiga nº 75,na cidade de Pelotas, estado do Rio Grande do Sul.

Para o desenvolvimento deste trabalho dividimos a turma em quatro grupos de cinco elementos sendo distribuídos a cada grupo, um CD,uma fita métrica, régua e um compasso.

CD é a abreviação de compact disc (disco compacto).É um disco digital com leitura de raio laser considerado atualmente o mais popular meio de armazenamento de dados digitais principalmente música comercializada e software de computador recebendo, neste caso , o nome de CD-ROOM (usado para Instalação de programas, recursos de multimídia, fotos, literaturas, jogos, etc).Como foi desenvolvido também para armazenar música ,chamado de CD-DA, substituiu o disco de vinil com vantagens, pois é gravado digitalmente, ou seja, os sons são transformados em bits e bytes.Chegou no mercado na década de 80 desenvolvido conjuntamente pela Sony japonesa e pela Philips holandesa.

Tendo em vista, então, que a música está presente na vida de todos nós e principalmente no cotidiano dos jovens, podemos aplicar a Matemática utilizando esse contexto, despertando neles curiosidade e senso crítico. Nesta proposta os alunos foram estimulados a relacionar o CD com a Geometria calculando sua área com instrumentos de medidas diferentes.

CÁLCULO DA ÁREA DE UM CD

DESENVOLVIMENTO

1ª Etapa:

Utilizando quatro CD’s (um por grupo), denominado-os A,B,C,D, fita métrica e comparando-os a uma circunferência, isto é, os alunos mediram seus contornos e através da fórmula C =2 π r obtiveram os raios, e aplicando na fórmula da área do círculo A = πr² calcularam as áreas,montando assim a tabela:

CD	Compr.circunf.(cm)	Raio(cm)	Área(cm²)
A	38,0	6,05	114,93
B	39,0	6,21	121,09
C	38,5	6,13	117,99
D	38,7	6,16	119,14

Calcularam, então, a média das áreas somando-as e dividindo pelo nº de CD’s, obtiveram 118,28 cm².

2ª Etapa:

Num segundo momento calcularam a área, medindo o diâmetro do CD,com uma régua,chegando assim aos resultados, conforme tabela:

CD	Diâmetro(cm)	Raio(cm)	Área(cm²)
A	12,2	6,10	116,83
B	11,9	5,95	111,16
C	12,1	6,05	114,93
D	11,8	5,90	109,30

Fizeram a média entre as áreas e obtiveram 113,05 cm².

3ª Etapa:

Num terceiro momento, foi solicitado aos grupos que reproduzissem o CD numa folha usando os instrumentos de medida entregues anteriormente. Levando em consideração que o centro do CD é representado por um círculo (conforme figura).

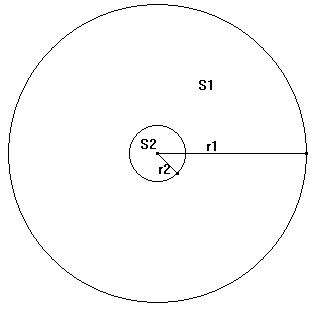
Calcularam as respectivas áreas montando a tabela:

CD	R₁	R₂	S₁	S₂	S_CD(S₁-S₂)
A	6,0	0,8	113,04	2,00	111.04
B	6,1	0,8	116,83	2,00	114,83
C	5,9	0,8	109,30	2,00	107,30
D	6,1	0,8	116,83	2,00	114,83

Da mesma forma, calcularam a média das áreas resultantes e obtiveram

111,86 cm².

Após os cálculos efetuados pelos grupos reproduzimos todo o processo com os alunos tentando verificar o cálculo real da área de um CD, e assim podermos comparar qual a média mais próxima da encontrada pelo grande grupo.

CÁLCULO DA ÁREA DE UM CD

Utilizando compasso e régua, calculou-se a área de um CD:

S₁= πr² com π=3,14

r=6,0 cm logo S₁=3,14.(6,0)² S₁= 113,4 cm²

S₂= πr²

r=0,75cm logo S₂=3,14.(0.75)²S₂= 1,76

ÁREA DE UM CD = (S₁-S₂)

S₁-S₂ = 113,4 – 1,76

S₁-S₂ = 111,64

CONCLUSÃO

O trabalho realizado possibilitou-nos uma análise sobre a utilização dos instrumentos de medidas, as quais podem ser observadas nas tabelas, pois com os mesmos instrumentos os grupos obtiveram medidas diferentes, resultando com isso cálculo de áreas distintas.

Tendo em vista que os valores encontrados pelos grupos foram divergentes, foi através da reprodução do processo juntamente com os participantes e comparando com os cálculos da 3ª etapa que chegamos a uma análise mais próxima da realidade.

Salientamos, também, que a diferença entre as medidas com a fita métrica deu-se pelo fato que a mesma sofre dilatação, pela ação do tempo e pelo material que é composta a fita.

Assim, concluímos que a média das áreas que mais se aproxima da área do CD foi a encontrada na 3ª etapa, pois além de utilizar a reprodução do mesmo com régua e compasso também foi considerado o centro do CD como um círculo.

ESTATÍSTICA

“PERFIL DO ALUNO QUE FREQÜENTA CINEMA”

ADÃO REINALDO VASCONCELOS ALVES

MARLENE BRUM GUAZINA

Pelotas, maio de 2006

INTRODUÇÃO

O presente trabalho tem por objetivo a construção de tabelas e gráficos a partir de um banco de dados. O estudo envolveu os professores Adão Reinaldo Vasconcelos Alves e Marlene Brum Guazina, da disciplina de Matemática, que desenvolvem seus trabalhos no Ensino Médio da Rede Estadual de Ensino e vinte alunos do 3º ano, noturno, da Escola Técnica Estadual Professora Sylvia Mello, localizada no bairro Fragata à rua Evaristo da Veiga, 75 na cidade de Pelotas, estado do Rio Grande do Sul.

A escola como Instituição representativa dos moradores do bairro, também recebe alunos oriundos das cidades próximas, tais como: Arroio Grande, Canguçu, Capão do Leão, Pedro Osório e São Lourenço do Sul. A escola possui 28 salas de aula, 114 professores, 18 funcionários, 1.698 alunos, 1 laboratório de informática, 1 biblioteca, 1 sala de vídeo, 1 quadra de esportes, 1 refeitório, 1 auditório, 1 laboratório de Biologia, 1 sala de jogos, sala dos professores, secretaria, SOE, SSE, setor pessoal.

Realizamos este trabalho com a intenção de fazermos uma coleta de dados através de uma pesquisa de campo, a fim de termos um perfil do nosso “aluno” nos finais de semana. A escolha da amostra foi feita com os alunos da escola a qual o entrevistado pertence. Num segundo momento organizou-se em tabelas os dados coletados e construiu-se planilhas e gráficos para representar os resultados obtidos e posteriormente divulgá-los a comunidade escolar.

QUESTIONÁRIO

TEMA:

CINEMA

PÚBLICO ALVO:

Alunos do 3º Ano do Ensino Médio,noturno, da Escola Técnica Estadual Professora Sylvia Mello.

OBJETIVO:

Colher dados, para analisar e interpretar gráficos e tabelas.

Dados de Identificação

Nome da Escola: Escola Técnica Estadual Professora Sylvia Mello

Cidade: Pelotas

Estado: RS

Rede: Pública

Série: 3º

Grau: Ensino Médio

Nome do aluno(a): _______________________________________
Sexo

a) ( ) Masculino

b) ( ) Feminino

3. Qual a sua idade? ______________________

4. Estado civil:

a) ( ) Solteiro(a)

b) ( ) Casado(a)

5. Meio de transporte usado para ir ao cinema.

a) ( ) Carro

b) ( ) Ônibus

6. Qual a renda mensal familiar(salário mínimo)? ___________________

Planilha: Banco de dados
Entrevistado	Idade	Estado civil	Transporte	Renda familiar em nº sal. mínimos
1	28	casado	carro	1
2	38	casado	carro	2
3	24	solteiro	carro	2
4	43	casado	carro	3
5	32	solteiro	ônibus	3
6	19	solteiro	ônibus	1
7	22	solteiro	ônibus	1
8	25	solteiro	ônibus	1
9	41	casado	ônibus	2
10	40	solteiro	ônibus	3
11	35	solteiro	carro	2
12	29	casado	carro	1
13	31	casado	carro	2
14	36	casado	carro	2
15	48	casado	carro	3
16	23	casado	carro	2
17	27	solteiro	ônibus	2
18	26	solteiro	ônibus	3
19	29	casado	ônibus	3
20	30	casado	carro	3
Fonte Aula de Matemática

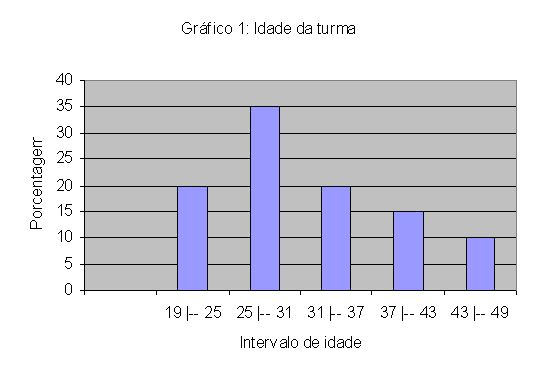
Tabela 1: Idade da turma
Idade	Freqüência absoluta	Freqüência relativa	Porcentagem (%)
19 \|-- 25	4	0,20	20
25 \|-- 31	7	0,35	35
31 \|-- 37	4	0,20	20
37 \|-- 43	3	0,15	15
43 \|-- 49	2	0,10	10
Total	20	1,00	100
Fonte: Aula de Matemática

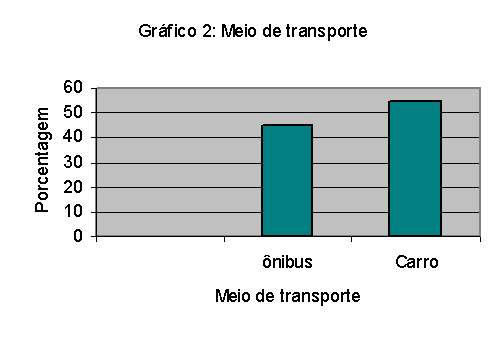
Tabela 2: Meio de transporte usado pela turma
Transporte	Freqüência absoluta	Freqüência relativa	Porcentagem (%)
ônibus	9	0,45	45
Carro	11	0,55	55
Total	20	1,00	100
Fonte: Aula de Matemática

Fonte: Aula de Matemática

Renda familiar nº sal. Mínimos

Média	2,1
Erro padrão	0,176217569
Mediana	2
Modo	2
Desvio padrão	0,788068926
Variância da amostra	0,621052632
Curtose	-1,307827929
Assimetria	-0,186395695
Intervalo	2
Mínimo	1
Máximo	3
Soma	42
Contagem	20

Figura 1-Resultado da Estatística Descritiva

Análise de Dados

Idade

Média	31,3
Erro padrão	1,729162
Mediana	29,5
Modo	29
Desvio padrão	7,733046
Variância da amostra	59,8
Curtose	-0,415549
Assimetria	0,520872
Intervalo	29
Mínimo	19
Máximo	48
Soma	626
Contagem	20

Figura 2-Resultado da Estatística Descritiva

Análise de dados

Estado Civil da Turma
Estado civil	Dados	Total
casado	Estado civil (%)	55,00%
	Estado civil (contagem)	11
solteiro	Estado civil (%)	45,00%
	Estado civil (contagem)	9
Total Estado civil (%)		100,00%
Total Estado civil (contagem)		20

Fonte: Aula de matemática

Tabela cruzada: Idade, transporte, renda familiar, estado civil.
Estado civil	Transporte	Dados	Total
Casado	Carro	Contagem de Idade	45,00%
		Contagem de Transporte	9
		Soma de Renda familiar em nº sal. Mínimos	19
	Ônibus	Contagem de Idade	10,00%
		Contagem de Transporte	2
		Soma de Renda familiar em nº sal. Mínimos	5
casado Contagem de Idade			55,00%
casado Contagem de Transporte			11
casado Soma de Renda familiar em nº sal. mínimos			24
Solteiro	Carro	Contagem de Idade	10,00%
		Contagem de Transporte	2
		Soma de Renda familiar em nº sal. Mínimos	4
	Ônibus	Contagem de Idade	35,00%
		Contagem de Transporte	7
		Soma de Renda familiar em nº sal. Mínimos	14
solteiro Contagem de Idade			45,00%
solteiro Contagem de Transporte			9
solteiro Soma de Renda familiar em nº sal. Mínimos			18
Total Contagem de Idade			100,00%
Total Contagem de Transporte			20
Total Soma de Renda familiar em nº sal. Mínimos			42

Fonte: Aula de matemática

CONCLUSÃO

Na sociedade moderna cada, vez mais interligada e homogênea, é possível conhecer com bastante precisão as tendências e preferências de consumo da maior parte da população, mediante as pesquisas de opinião.

Aplicadas em grupos reduzidos (amostras representativas), as pesquisas levantam informações fidedignas sobre as atitudes de determinado grupo em relação a um assunto ou situação concreta. Para isso, as etapas consideradas importantes da pesquisa foram: definição do universo; escolha da amostra; elaboração do questionário; entrevista a pessoas da comunidade escolar(alunos); tabulação; análise e interpretação dos resultados.

No questionário procuramos fazer perguntas que não irritassem ou ferissem o entrevistado, obedecendo a uma ordem lógica, de modo que as respostas obtidas correspondessem a um questionário claro e lógico, já que a entrevista é um ponto delicado, que requer muita habilidade. As perguntas do questionário foram objetivas, para que o entrevistador inexperiente não induzisse o entrevistado a dar uma resposta seguida por ele, ainda que inconscientemente, pois um tipo de resposta distorcida poderia contribuir para falsear os resultados da pesquisa.

SITUAÇÃO DE ESTUDO DE UM CD EM OUTRAS DISCIPLINAS

Este trabalho pretende oportunizar reflexões relacionadas com a Modelagem Matemática, visando a sua viabilidade para o ensino da Matemática nos diferentes níveis.

A Modelagem Matemática, enquanto estratégia alternativa para o ensino matemático num ambiente contextualizado desempenha função importante na Educação Matemática, pois representa uma perspectiva que inclui as vivências sócio-escolares, construção e consolidação do conhecimento garantindo aprendizagens significativas.

Esse processo que envolve a realidade e a Matemática mediante o qual se definem estratégias de ação, proporcionando ao aluno uma análise global da realidade em que ele interage.

A situação de estudo, considerada o inicio de um processo de descrição da situação real num problema passa a desencadear o nosso trabalho, partindo do estudo de um CD.

Este tema levou o aluno a um ambiente de motivação e envolvimento, a analisar o problema, possibilitando resolver aquilo que estivesse ao seu alcance, buscando a construção do conhecimento, conduzindo-o por fim a conquista de seus objetivos.

Este trabalho teve a participação da disciplina de Física onde foi estudado o funcionamento básico de um CD, em alguns tópicos da Física, tais como: reflexão da luz, recepção de ondas luminosas, codificação das ondas luminosas em sinais elétricos.

A disciplina de Química contribuiu com a pesquisa do material que compõem o CD (graváveis – regraváveis): rótulo (papel ou impresso); camada plástica protetora;camada refletida com relevo plano; camada dielétrica para disparar calor do laser durante a gravação; camada gravável-regravável: transparente,pode ter pontos tornados opacos ( disco gravável uma única vez) e vice-versa ( discos regraváveis) e camada de policarbonato. A comparação do CD como um modelo atômico. As linhas representam os níveis eletrônicos, onde estão localizados os elétrons e o círculo menor do CD representa o núcleo do átomo.

Dentro da disciplina de Biologia, podemos estudar a influência do som no aparelho auditivo.

E também tivemos a participação da disciplina de Língua Portuguesa na produção de textos.