---

2. LEIS DA REFLEXÃO

A reflexão da luz é um fenômeno físico que consiste na mudança de direção dos raios de luz incidentes sobre uma superfície refletora, exceção feita à situação na qual o ângulo de incidência seja igual a 90^o, em que a direção se mantém, mas, apenas o sentido da propagação se altera.

Em síntese são duas as Leis da Reflexão da Luz:

 

1a Lei: O ângulo de incidência () é igual ao ângulo de reflexão ()

2a Lei: O Raio Incidente I, a normal à superfície refletora (N) e o raio refletido (R) estão no mesmo plano.

Considere uma reta N, perpendicular à superfície refletora que denominaremos Normal à superfície.

---

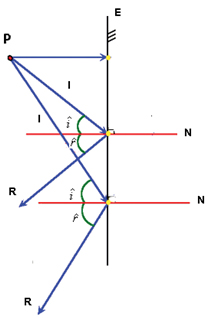
3. CONSTRUÇÃO DE IMAGENS NOS ESPELHOS PLANOS

Vamos estudar a construção de imagens conjugadas por um espelho plano a partir de um ponto considerado objeto.

Consideremos, portanto, um ponto P, diante de um espelho plano E, como indica a figura a seguir:

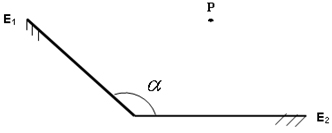
Figura 6 - Ponto P diante de um espelho plano E.

Se admitirmos raios de luz incidentes I sobre o espelho E, passando pelo ponto P, temos que considerar a existência de raios de luz refletidos R, de forma tal, que os ângulos de reflexão serão iguais aos ângulos de incidência (1^a Lei de Reflexão), como está indicado na figura a seguir.

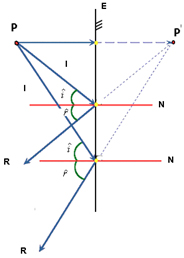
Figura 7 - Traçado de luz dos raios incidentes e refletidos

Para determinarmos o ponto imagem P´, basta que façamos um prolongamento dos raios de luz refletidos. A convergência desses pontos é P´. Observe a figura a seguir:

 

Figura 8 - Determinação gráfica do ponto imagem P´

Pode-se perceber que a distância do ponto P ao espelho E é igual a distância do espelho E ao ponto imagem P´ (PE = EP´), ou seja, a imagem P´ é simétrica ao ponto P.

 

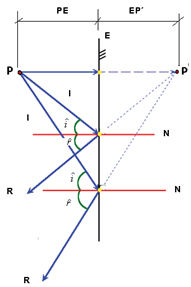
Figura 9 - Simetria do ponto imagem P´ em relação ao ponto objeto P

Além disso, como o ponto imagem P´é formado pelo prolongamento dos raios de luz, podemos dizer que ele é virtual.

---

4. ENANTIOMORFISMO

Como vimos as imagens conjugadas por espelhos planos são simétricas aos objetos, isto é, a distância de cada ponto do espelho ao objeto é igual à distância da imagem ao espelho, o que nos permite concluir que apesar da imagem ter o mesmo tamanho do objeto eles não são exatamente iguais. Na verdade a imagem fica invertida em relação ao objeto. Esse fenômeno recebe o nome de enantiomorfismo.

---

5. TRANSLAÇÃO DE UM ESPELHO PLANO

Quando movemos um espelho a imagem por ele conjugada também se movimenta.
Considere um objeto P localizando a uma distância d₁ de um espelho E, como indica a figura a seguir.

Como espelhos planos conjugam imagens simétricas em relação ao objeto, temos que a imagem P´, também se encontra a ima distância d₁ do espelho.

Se deslocarmos o espelho de um certa distância a, então teremos

Perceba que a distância X entre as duas posições sucessivas das imagens P´e P´´ pode ser expressa por:

 

          (1)

Observe a figura 12 e perceba que:

Então:

X = 2a          (2)

Dessa forma conclui-se que o deslocamento da imagem é o dobro do deslocamento do espelho.

---

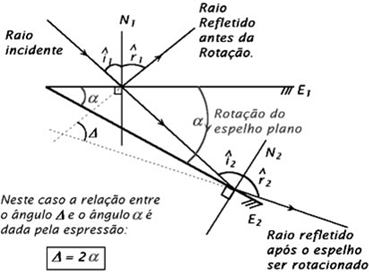
6. TROTAÇÃO DE UM ESPELHO PLANO

Se ao invés de deslocar o espelho de uma distância a, nós o girarmos de um certo ângulo , podemos mostrar, de maneira análoga que giramos a imagem de um ângulo D= 2a.

Figura 14 - Rotação do espelho plano

Fonte: http://www.brasilescola.com/upload/e/reflexao4.jpg

 

---

7. ASSOCIAÇÃO DE ESPELHOS PLANOS

Quando associamos dois espelhos planos de forma paralela, um em relação ao outro, ou de maneira a formarem ângulos entre si, nós podemos multiplicar o número de imagens conjugadas de um determinado objeto.

Assim, se consideramos dois espelhos planos E₁ e E₂ que formam entre si um ângulo a, como está indicado na figura a seguir.

 

Figura 15 - Associação de espelhos planos

O número n de imagens de P que essa associação pode conjugar é igual a:

          (4)

Perceba que se for igual a 180^o então, temos, na prática apenas um espelho e, portanto, n=1, ou seja, há a conjugação de uma única imagem.

Para a igual a zero temos que os espelhos estão paralelos e, dessa forma, matematicamente teríamos uma impossibilidade. Entretanto, se pensarmos em um valor muito pequeno para am então perceberemos que n seria igual a infinito, ou seja, infinitas imagens. Isso só seria possível se o sistema não absorvesse energia.

Essa expressão só é válida para valores de a que sejam submúltiplos de 360^o. Caso contrário o número de imagens não é inteiro.