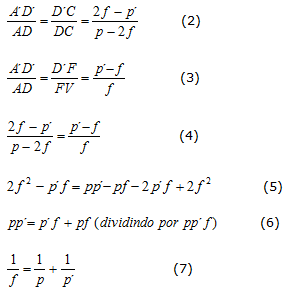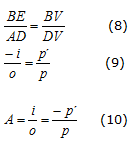Nós estamos acostumados a utilizar espelhos planos em nossa casa, mas, o nosso cotidiano está repleto de situações nas quais fazemos uso dos espelhos esféricos. Observe, nas figuras a seguir, as aplicações cotidianas dos espelhos esféricos.

Os dentistas, para poderem enxergar melhor os dentes de seus pacientes, utilizam espelhos esféricos.

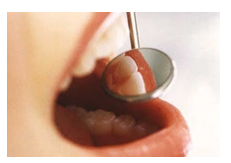
Figura 1 - Espelho esférico utilizado pelo dentista

Fonte: www.infoescola.com/fisica/espelhos-concavos/

Os espelhos utilizados nos retrovisores dos automóveis (figura 2) e nos elevadores e lojas (figura 3), são esféricos tendo em vista o fato de possibilitarem um maior campo de visão quando comparados aos espelhos planos.

Figura 2 - Espelho esférico utilizado no retrovisor de um carro

Fonte: www.efetividade.net/.../

Figura 3 - espelhos esféricos utilizados em lojas ou em porta de elevadores

Fonte: www.mundoeducacao.com.br/fisica/espelhos-esfe...

Para entendermos o que é um espelho esférico, considere uma esfera cuja superfície reflete a luz, conforme a figura 1, a seguir.

Figura 1 - Esfera refletora seccionada ao meio gerando espelhos esféricos.

Fonte: cepa.if.usp.br/.../basico/cap05/cap5_01.php

Dividindo essa esfera em duas partes, obtemos duas calotas esféricas. Cada uma delas apresenta uma superfície côncava e outra convexa. Assim, os espelhos esféricos podem ser classificados em côncavos e convexos, como indica a figura 2.

Figura 2 - Espelhos esféricos: côncavo e convexo.

Fonte: cepa.if.usp.br/.../basico/cap05/cap5_01.php

Diferentemente das lentes esféricas, que são atravessadas pelos raios de luz incidentes, nos espelhos esféricos os raios de luz não os atravessam. Quando um feixe de raios de luz paralelos incide sobre um espelho, ocorre o fenômeno de reflexão.
Se as condições de Gauss forem respeitadas (veja o software "Um mano chamado Gauss"), então todos os raios de luz incidentes no espelho esférico serão refletidos por ele de maneira a passarem por um único ponto denominado foco do espelho (F). A distância desse ponto ao espelho é chamada de distância focal (f), e a distância entre o centro de curvatura do espelho (C) e seu vértice (V) é chamada de raio de curvatura do espelho (R). No caso do espelho convexo, é o prolongamento do raio de luz incidente que passa pelo foco.

Figura 3 - Características dos espelhos esféricos.

É possível notar, pela figura 3, que no espelho côncavo, os raios de luz tendem a convergir para o foco do espelho. Por isso dizemos que nos espelhos côncavos, o foco é real.
No caso dos espelhos convexos, os raios de luz tendem a divergir, contudo, os prolongamentos dos raios incidentes tendem para o foco. Por isso dizemos que nos espelhos convexos, o foco é virtual.

Uma relação interessante e válida, tanto para os espelhos côncavos quanto para os espelhos convexos, é que a distância focal é a metade do raio de curvatura do espelho esférico. Observe a figura 4 a seguir, admitindo F como sendo o foco do espelho, C o centro de curvatura do espelho, V o vértice do espelho, R o raio de curvatura do espelho, I o ponto de incidência da luz no espelho, e , os ângulos de incidência e de reflexão, respectivamente.

Figura 4 - Relação distância focal e raio de curvatura.

Como no fenômeno da reflexão o ângulo de incidência é igual ao ângulo de reflexão, podemos considerar o triângulo CFI isósceles, portanto, FC = FI.
Para cumprir as condições de nitidez de Gauss, o ângulo de abertura do espelho deve ser pequeno, em torno de 10o, dessa forma, FI @ FV.
Portanto, podemos concluir que:

          (1)

Antes de discutirmos o processo de construção das imagens, é importante conhecermos as propriedades dos raios de luz incidentes nos espelhos esféricos.

A primeira propriedade, nós já discutimos, pois diz respeito ao fato de que todo raio de luz incidente em um espelho esférico, ao refletir, passa pelo foco.
Considere a figura a seguir, onde C é o centro de curavtura do espelho, F é o foco do espelho e V o vértice do espelho.

Figura 5 - Raio de luz incidindo sobre o foco de espelhos esféricos.

A segunda propriedade diz respeito ao fato de os raios de luz incidentes que passam pelo centro da curvatura (C) de uma lente esférica refletirem passando por si mesmos.

Figura 6 - Raio de luz incidindo sobre o centro de curvatura de espelhos esféricos.

Como já foi estudado no software "conhecendo as lentes delgadas", as imagens conjugadas pelo encontro de raios de luz são denominadas reais, enquanto que, a imagens conjugadas pelo encontro do prolongamento dos raios de luz são denominadas virtuais.

A terceira propriedade diz respeito ao fato de os raios de luz incidentes, que passam pelo vértice do espelho esférico, refletirem com o mesmo ângulo no qual ocorreu a incidência.

Figura 7 - Raio de luz incidindo sobre o vértice de espelhos esféricos.

As imagens fornecidas por um espelho esférico podem ser obtidas utilizando-se dois dos três raios particulares.
Obs.: trataremos aqui apenas de imagens formadas for objetos reais.

Objeto extenso localizado na frente do espelho: imagem virtual, direita, menor.

Figura 8 - Formação de imagens em espelhos esféricos convexos.

Observe que as características da imagem A'B' para o espelho convexo não dependem da posição do objeto AB sobre o eixo principal.

Objeto extenso à esquerda do ponto C (Objeto além do centro): imagem real, invertida, menor.

Figura 9 - Formação de imagens em espelhos esféricos côncavos com o objeto à esquerda do centro de curvatura do espelho.

Objeto extenso sobre C (Objeto colocado no centro de curvatura do espelho): imagem real, invertida, igual.

Figura 10 - Formação de imagens em espelhos esféricos côncavos com o objeto sobre o centro de curvatura do espelho.

Objeto extenso entre C e F (Objeto colocado entre o centro de curvatura e o foco): imagem real, invertida, maior.

Figura 11 - Formação de imagens em espelhos esféricos côncavos com o objeto colocado entre o centro de curvatura do espelho e seu foco.

Objeto extenso sobre F (Objeto colocado no foco do espelho): imagem imprópria, também dita no infinito.

Figura 12 - Formação de imagens em espelhos esféricos côncavos com o objeto colocado sobre foco do espelho.

Objeto extenso entre F e V(Objeto colocado entre o foco e o vértice): imagem virtual, direita, maior.

Figura 13 - Formação de imagens em espelhos esféricos côncavos com o objeto colocado à direita do foco do espelho.

Observe que:

• as características da imagem A'B' para o espelho côncavo dependem da posição do objeto AB sobre o eixo principal.
  
• a imagem do ponto B está sobre o eixo principal.
  
• para qualquer tipo de espelho, uma imagem real será sempre invertida, enquanto uma imagem virtual será sempre direita.

Para estudarmos as características das imagens conjugadas por espelhos esféricos, Gauss deduziu uma equação semelhante a que utilizou para estudar as lentes esféricas. A seguir, apresentamos a dedução de Gauss.

Figura 14 - Imagem conjugada por um espelho esférico côncavo.

Podemos observar que o triângulo ADC é semlehante ao triângulo A´D´C e que o triângulo A´D´F é semelhante ao triângulo BFV, portanto:

Considere a imagem conjugada por um espelho esférico côncavo:

Figura 15 - Ampliação da imagem por um espelho esférico côncavo.

Observe que os triângulos ADV e BEV são semelhantes, portanto, podemos escrever:

Analisando a equação 10, podemos afirmar que:

Se A for maior que zero, ou seja, positivo, então i e o têm o mesmo sinal, portanto a imagem é direita.

Se A for menor que zero, ou seja, negativo, i e o têm sinais contrários, portanto a imagem é invertida.
Em resumo ao estudo dos espelhos esféricos, podemos afirmar que, considerando sempre o objeto real ( p > 0 ), nestas equações temos:

Espelho côncavo f > 0
Espelho convexo f < 0
Imagem real p' > 0
Imagem virtual p' < 0
Imagem direita i > 0
Imagem invertida i < 0