|
1.
O POSTULADO DE DE BROGLIE
e ainda considerando que o fóton não
existe em repouso, isto é, sua massa de repouso é
nula, mo=
0, temos
ou A expressão mostra o momento associado ao fóton. O comprimento de onda da onda associada ao seu movimento é Em 1924, Luiz De Broglie propôs a existência de ondas de matéria, ou seja, o caráter dual não era somente uma característica da luz. Por simetria, De Broglie postulou que uma partícula de matéria tem uma onda associada ao seu movimento tal que
onde lDB é o comprimento de onda de De Broglie de uma onda de matéria associada ao movimento de uma partícula material que tem momento p. As idéias de De Broglie não tinham evidências experimentais na época. Cerca de cinco anos mais tarde, a quantidade de resultados de experiências motivadas por suas ideias e que confirmavam as hipóteses era tão grande que ele ganhou o Prêmio Nobel de Física.
Esse comprimento de onda é tão pequeno que não pode interagir com nenhum sistema conhecido, redes de difração, por exemplo. É impossível evidenciar o caráter ondulatório nesse caso. Porém, imagine agora elétrons que possuem massa 9,1 x 10-31 kg com uma energia de 100 eV (1 eV é a energia adquirida por um elétron quando acelerado por uma ddp de 1V).
Esse comprimento de onda, da ordem de 1Ao (1 angstron=10-10 m), é próximo ao comprimento de onda de raios X. Por volta de 1912, Max von Laue elaborou um experimento para realizar difração de raios X, utilizando uma estrutura cristalina como rede de difração tridimensional. Logo depois William Henry Bragg e seu filho William Lawrence Bragg demonstraram a relação que passou a ser conhecida como Lei de Bragg, fundamental para o estudo de estruturas cristalinas com o uso da difração de raios X. |
| 1.1
Difração de elétrons A
difração de raios X em cristais permitia determinar
a distância entre diferentes planos interatômicos de
acordo com a Lei de Bragg. Cristais são estruturas caracterizadas
por um arranjo periódico e bem ordenado de seus componentes.
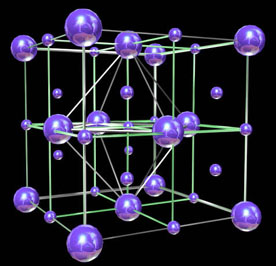
A figura 1 mostra a regularidade dos átomos dispostos num
cristal e a figura 2 mostra o caminho das ondas de raios X.
Figura 1: Estrutura de um cristal: a distância
interatômica é regular.
Figura 2: Lei de Bragg para a difração
de RX num cristal.
Lei de Bragg: Nl = 2 d sen q (7) A Lei de Bragg exprime o fenômeno de interferência
construtiva entre ondas que são refletidas por uma rede cristalina
e tem uma diferença de caminho ótico igual a um múltiplo
inteiro N
de l. A distância
d entre os planos interatômicos pode ser
determinada se l é conhecido.
A figura 3 é uma foto do resultado obtido quando um feixe
de raios X atravessa uma fina folha de ZrO2 (óxido
de zircônio). Os anéis claros são resultantes
das interferências construtivas das ondas de raios X.
Figura 3 - Difração de Raios X em cristais de óxido de zircônio. Fonte: Eisberg e Resnick, 1994
Figura 4: Esquema do método de G. P. Thomson
para obter a Difração de elétrons. A figura 5 mostra o resultado obtido. A formação do padrão de difração, isto é, a produção de anéis de interferência construtiva e a coincidência entre o comprimento de onda previsto pela Lei de Bragg por meio da hipótese de De Broglie comprovaram a hipótese da natureza ondulatória dos elétrons. (DIFRAÇÃO..., 2009).
Figura 5 - Difração de elétrons
em cristais de ouro. Por meio da medição do raio do anel
de interferência, foi possível determinar as distâncias
interatômicas conhecidas de cristais tais como a grafite.
No esquema a seguir, r é o raio do anel e l é a distância
entre o cristal e a tela de projeção. (ESTRUTURA...,2009).
Figura 6: Relação entre o raio do
anel e a distância interatômica do cristal. Da figura 6 temos: Como o ângulo a
é bem menor que 10o , podemos dizer que r'
Na figura 2, vimos que o ângulo a corresponde ao ângulo 2q da Lei de Bragg. Substituindo, teremos:
como a=2q teremos:
Para as condições estabelecidas (da montagem), temos q menor que 50 e isto permite aproximar a relação acima na seguinte expressão:
mas de acordo com a Lei de Bragg:
Então:
Logo, a distância interatômica pode ser determinada se l é conhecido e r é medido experimentalmente, pois
A partir da constatação da difração dos elétrons e, mais tarde, de prótons e nêutrons (apesar de serem bem mais massivos do que o elétron e por isso mais difícil a observação do comportamento ondulatório), concluiu-se que todas as partículas de matéria têm comportamento dual. Neils Bohr, que já havia utilizado o comportamento dual da radiação eletromagnética em seu modelo atômico, generalizou o conceito de dualidade através do Princípio da Correspondência:
REFERÊNCIAS
|
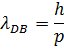 (5)
(5)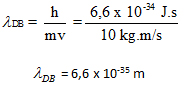
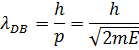 (6)
(6)
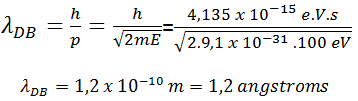


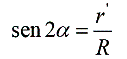 (8)
(8)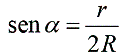 (9)
(9)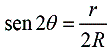 (10)
(10)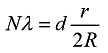 (13)
(13)