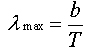T E O R I A     (Referencial Físico Matemático)
Imprimir Imprimir
1. O ESPECTRO DE RADIAÇÃO DO CORPO NEGRO

De acordo com a Lei da radiação de Kirchhoff, se um corpo puder absorver toda a radiação incidente sobre ele, então emitirá toda a radiação por ele gerada. Este corpo ideal é conhecido como corpo negro. Uma boa aproximação para um corpo negro é obtida num forno de paredes internas enegrecidas, com um pequeno orifício por onde a radiação gerada é emitida. A análise dessa radiação é feita através de um espectrômetro, como mostra a figura 1 a seguir, medindo a intensidade da radiação para cada comprimento de onda do espectro contínuo emitido.



Figura 1 - Equipamento para a análise da radiação emitida por um corpo negro.


No final do século XIX, muitos cientistas estavam preocupados em explicar porque os espectros dos corpos negros são tão parecidos com os espectros emitidos por corpos aquecidos, tais como o filamento de uma lâmpada, isto é, porque todos esses espectros dependiam da temperatura do corpo. A figura a seguir mostra as curvas da intensidade da radiação do corpo negro em função do comprimento de onda para diferentes temperaturas. (Figura 2)


Figura 2 - Curvas de emissão de radiação em função do comprimento de onda de um corpo negro para diferentes temperaturas.
Fonte: http://docs.kde.org/stable/pt/kdeedu/kstars/ai-blackbody.html
Essas curvas, e também as curvas obtidas para corpos aquecidos não negros, apresentam outras propriedades que ficaram conhecidas como Leis de Stefan-Boltzmann e Wien.

1.1 LEI DE STEFAN-BOLTZMANN

A partir dos resultados experimentais obteve-se a relação entre a potência total irradiada por um corpo negro para todos os comprimentos de onda, a área da superfície emissora e a temperatura absoluta. Essa relação empírica é dada por :

Esta função expressa que a Intensidade total da radiação emitida é proporcional à quarta potência da temperatura de equilíbrio térmico do corpo, onde s é uma constante universal conhecida por constante de Stefan-Boltzmann, cujo valor é:

Para um corpo aquecido qualquer, tal qual o filamento de uma lâmpada, multiplica-se a expressão da Lei de Stefan-Boltzmann pela constante e, correspondente à emissividade.

1.2 LEI DE DESLOCAMENTO DE WIEN

 O ponto máximo da curva I x l, vista acima, se desloca de acordo com a seguinte expressão:


Pela expressão acima se depreende que o pico da curva se desloca de modo que lmax diminui quando a temperatura aumenta, onde b é uma constante cujo valor é: 


Para explicar esses resultados, os cientistas utilizavam o modelo dos osciladores, no qual se entende que a radiação térmica é constituída por ondas eletromagnéticas emitidas devido à agitação térmica (teoria eletromagnética clássica de Maxwell). Por esse motivo, a radiação térmica dependeria da temperatura do corpo, isto é, um aumento na temperatura provocaria o aumento da amplitude de oscilação das partículas. As ondas eletromagnéticas emitidas teriam mais energia, que poderia variar dentro de uma faixa contínua de valores, e por isso o espectro de emissão seria contínuo, contendo todos os comprimentos de onda do espectro contínuo. Porém, as equações obtidas a partir desse modelo levaram a uma curva teórica que coincidia com os resultados experimentais apenas para os comprimentos de onda longos, na região do infravermelho. A discordância na região de comprimentos de onda curtos ficou conhecida como catástrofe do ultravioleta. A figura a seguir mostra o resultado experimental e a tentativa fracassada de reproduzi-lo.

1.3 PLANCK E A QUANTIZAÇÃO DE ENERGIA

Em 1900, Max Planck estudou detalhadamente os espectros obtidos a partir de altos fornos de siderúrgica na Alemanha e conseguiu resolver o problema. Na verdade, Planck introduziu um postulado no modelo dos osciladores, isto é, o conceito introduzido não era consequente de nenhuma lei até então conhecida.
De acordo com o postulado, os osciladores não poderiam oscilar com qualquer valor de energia, ou seja, não poderiam variar sua energia continuamente entre zero e um valor máximo. Planck postulou que existiria um valor mínimo para a energia que seria absorvida ou emitida pelo corpo negro. Esse valor foi denominado quantum de energia que, por sua vez, é proporcional à frequência de oscilação:

onde h é uma constante de proporcionalidade, que ficou conhecida por constante de Planck. A energia total dos osciladores era obtida a partir da soma desses quanta, ou seja:

O próximo passo foi relacionar as energias dos osciladores com as ondas eletromagnéticas emitidas pelo corpo negro: se a energia dos osciladores é quantizada, então, a energia das ondas emitidas também é. Ao calcular a energia total das ondas emitidas, Planck obteve uma equação cujos resultados coincidem com os resultados experimentais quando a constante h assume um valor correspondente a:


1.3.1 Interpretação da quantização de energia de Planck

O resultado obtido por Planck, apesar de estar de acordo com os resultados experimentais para a radiação do corpo negro, deveria ser aplicado a qualquer tipo de oscilador e isso contrariava leis até então indiscutivelmente válidas: as Leis de Newton, que permitiam que a energia assumisse qualquer valor.

Porém, o que o postulado de Planck sugere é que a natureza, que sempre utiliza energia na menor quantidade possível, não pode utilizar uma quantidade infinitamente pequena. Essa energia tem um valor mínimo imposto pela constante h. Por isso não é possível observar variações tão pequenas de energia no mundo macroscópico.

O valor 6,63 x 10 -34 é muito pequeno para ser multiplicado pelas frequências de oscilação de corpos grandes, resultando em valores de energia imensuráveis. Somente no mundo microscópico, isto é, para partículas elementares como os elétrons, que podem oscilar em altíssimas frequências, é possível obter resultados de variações de energia mensuráveis!
Segundo essa idéia revolucionária, a luz emitida pelo Sol ou por uma lâmpada, por exemplo, é constituída por um enorme número de pacotes de energia, os quanta de luz, ou fótons. Cada fóton tem uma energia hv proporcional à frequência. Um fóton de luz ultravioleta é cerca de duas vezes mais energético que um fóton de luz vermelha, já que suas frequências são aproximadamente 10 x 10 14 Hz e 5 x 10 14 Hz, respectivamente.